Для выполнения тяговых расчетов в инженерной практике необходимо выбрать модель поезда, движущегося по железнодорожному пути, которая бы, с одной стороны, не была бы излишне сложной, а с другой стороны, обеспечивала бы необходимую точность. Поэтому в расчет вводятся следующие предпосылки и допущения.
1. Поезд представляется как материальная точка, расположенная в середине поезда, в которой сосредоточена вся масса состава. Рельсы выполняют роль внешних удерживающих связей, заставляющих поезд двигаться только в одном направлении, поэтому механическое движение поезда по железнодорожному пути можно описать как движение материальной точки с одной степенью свободы. Для описания такого движения достаточно одного дифференциального уравнения.
2. Для предсказания движения поезда достаточно учитывать только внешние силы. Работа внутренних сил неизменяемой системы равна нулю, потому что силы взаимно уравновешиваются, следовательно, их можно не учитывать при математическом описании движения. В тяговых расчетах учитываются только те внешние силы, которые совпадают с направлением движения поезда. Если такие силы приложены к одной точке, то их можно алгебраически складывать и рассматривать движение поезда под воздействием результирующей силы. К числу них относятся сила тяги, силы сопротивления движению и тормозная сила. Результирующую силы относят к одной тонне массы поезда и называют удельной.
3. Для удобства и простоты дальнейших рассуждений будем представлять поезд неким чёрным ящиком с точки зрения процессов происходящих внутри (см. рис. 1.1).
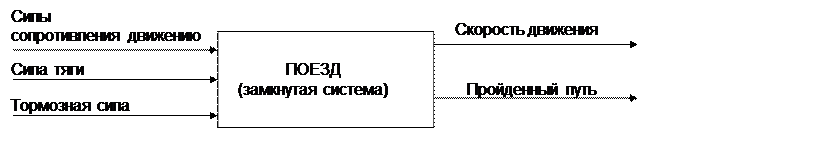
Рис. 1.1 Схема взаимодействия объекта «поезд» с внешней средой
Таким образом, предсказание движение возможно по входам и выходам системы без учета динамики процессов внутри системы, что позволяет использовать в расчетах статические характеристики сил тяги, торможения и сопротивления движению. При смене режимов управления или внешней нагрузки не учитывают изменение сил при переходе от одного установившегося процесса к другому.
4. Так как силы, действующие на поезд, зависят от скорости, то движение можно предсказать только путем решения дифференциальных уравнений. Для упрощения тяговых расчетов сложные нелинейные функции сил, зависящих от скорости, аппроксимируют кусочно-линейными, что позволит использовать принцип суперпозиции и решить дифференциальные уравнения в форме задачи Коши. Это означает, что непрерывную нелинейную функцию равнодействующих сил, зависящих от скорости движения, заменяют дискретной (прерывной) кусочно-линейной по малым интервалам скорости движения. Тогда в пределах каждого интервала можно принять силу постоянной и соответствующей средней скорости в интервале. Использование принципа суперпозиции означает, что в каждом интервале скорости допустимо принимать равнодействующую сил, действующих на поезд, постоянной по значению и соответствующей средней скорости в интервале и заданному режиму движения.
Построение математической модели представляет собой вывод дифференциального уравнения движения поезда согласно изложенной выше расчетной схеме.
Кинетическая энергия, Т, поезда, при условии, что колеса катятся без скольжения определяется по формуле:
|
|
(1.1) |
|||
|
где |
P+Q |
– |
масса поезда, равная сумме, соответственно, локомотива и вагонного состава |
|
|
v |
‑ |
скорость движения поезда |
||
|
I |
‑ |
момент инерции вращающихся частей относительно оси вращения |
||
|
ω |
‑ |
угловая скорость вращения вращающихся частей |
||
|
|
||||
|
где |
R |
– |
радиус колеса |
|
|
|
||||
|
где |
m |
‑ |
масса вращающихся частей |
|
|
ρ |
‑ |
радиус инерции вращающихся частей |
||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.