Уравнение движения поезда. Предпосылки и допущения к расчетной схеме, страница 2

Тогда

Обозначив суммарную массу вращающихся колесных пар через m_п, и выполнив подстановку, выражение (1) примет вид:

(1.2)

Обозначим:

Тогда, с учетом обозначение выражение (2) можно записать:

(1.3)

Выражение (1 + γ) называется коэффициентом инерции вращающихся масс поезда.

Изменение кинетической энергии поезда на некотором перемещении его составит:

(1.4)

Согласно предположению (1), приведенному в п. 1.1 работа внутренних сил поезда равна нулю, и поэтому ее не будем учитывать. Тогда, согласно закону сохранения энергии изменение кинетической энергии равно работе сил на пройденном пути:

,				(1.5)
где	Fk	–	касательная сила тяги локомотива;
	Wk	‑	общее сопротивление движению поезда;
	BT	‑	тормозная сила;
	s	‑	путь, пройденный поездом.

Выражение (F_k ‑ W_k ‑ B_T) является равнодействующей силой, которую будем обозначать

R = (Fk ‑ Wk ‑ BT)

Подставив выражение (3) в выражение (4), с учетом принятого обозначения получим:

,

(1.6)

Скорость движения поезда есть первая производная пройденного пути по времени:

,

(1.7)

Подставляя выражение (4) в выражение (3), и сокращая v получаем:

,

(1.8)

В тяговых расчетах принято использовать не силы как таковые, обозначаемые обычно прописными буквами латинского алфавита R, F_k, W_k, B_T, а удельные значения сил, т.е. отнесенные к массе, которые обозначаются строчными буквами, соответственно, r, f_k, w_k, b_T. Это сделано для упрощения расчетов. Кроме того, следует напомнить о различных системах единиц.

Если расчеты производятся в системе СИ, то масса измеряется в кг, расстояние – в м, время – в с, скорость в м/с, ускорение – в м/с², сила – в Н. На транспорте применяется техническая система единиц, в которой масса поезда измеряется в т, время – в ч, скорость в км/ч, ускорение в км/ч², сила в кГс (килограмм-силах).

Удельная равнодействующая сила в СИ будет равна:

,

(1.9')

а в технической системе, соответственно:

.

(1.9'')

Выражение (8) примет вид:

,

(1.10)

Определим величину ξ в СИ и в технической системе.

Значения γ определены для всех типов подвижного состава, эксплуатирующегося на железных дорогах РФ, и приведены в Правилах тяговых расчетов [ ]. В тяговых расчетах при проектировании железных дорог для груженого поезда можно принято γ=0,06.

Для системы СИ величина  ξ составляет:

,

Однако такая размерность очень неудобна в повседневном использовании, потому что массу поезда удобнее выражать в т, скорость движения – в км/ч, а ускорение – в км/ч². В этом случае величина ξ будет равна:

В технической системе единиц, соответственно, величина ξ = 12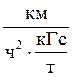

Таким образом, дифференциальное уравнение движения поезда примет следующий вид:

- в режиме тяги

(1.11)

- в режиме холостого хода

(1.12)

- в режиме торможения 

(1.13)