
Работа №3. Моделирование упругих деформаций образца в процессе ударного воздействия с использованием решателя дифференциальных уравнений ode45
I. Цель работы:
Научиться составлять систему дифференциальных уравнений движения для взаимодействующих тел и получать численное решение системы с использованием решателя дифференциальных уравнений ode45 системы MatLab.
II. Задание и порядок выполнения
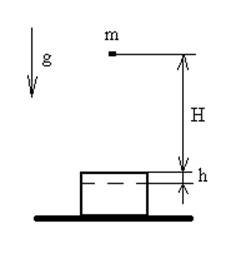
Образец горной породы, положенный на несжимаемое основание, испытывает динамическое нагружение несжимаемым грузом, падающим без начальной скорости с высоты H. При этом происходит упругая деформация образца только в направлении падения груза на величину h. Определить вид упругих деформаций образца (зависимость смещения верхней поверхности от времени) для различных коэффициентов затухания колебаний b.
 В
соответствии со вторым законом Ньютона имеем
В
соответствии со вторым законом Ньютона имеем ![]() , где k – коэффициент жесткости породы, определяемый
выражением
, где k – коэффициент жесткости породы, определяемый
выражением 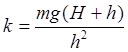 .
.
Для численного решения данного уравнения с помощью функции ode45, реализующей алгоритм Рунге – Кутта 4 – 5 – го порядка, необходимо его представить в виде системы дифференциальных уравнений первого порядка. Очевидно, что ускорение взаимодействующих тел следует выразить через их скорость, а скорость – через смещение. В итоге получим систему дифференциальных уравнений
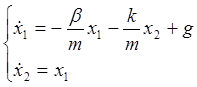
с
начальными условиями ![]() .
.
Полученную систему необходимо представить в виде отдельной функции, имя которой идет в качестве одного из аргументов функции ode45. Более подробную информацию об использовании функции ode45 можно получить, набрав команду help ode45.
III. Пример оформления
Примерный вид файла, содержащего текст функции, описывающей систему уравнений:
function F = Dif(t,x)
% Dif – это название функции, которое должно совпадать с именем
% файла
% k/m = -5.8802e+009, betta/m = -1e4, g = 9.8
F = [-1e4*x(1)-5.8802e+009*x(2)+9.8; x(1)];
Вид файла, содержащего текст вызова функции ode45 и отображения графика:
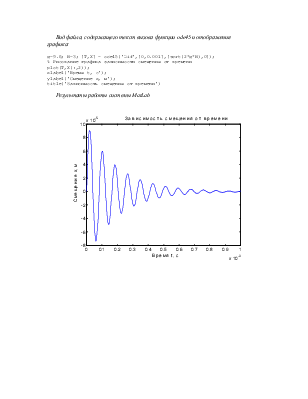
g=9.8; H=3; [T,X] = ode45('Dif',[0,0.001],[sqrt(2*g*H),0]);
% Рисование графика зависимости смещения от времени
plot(T,X(:,2));
xlabel('Время t, с');
ylabel('Смещение x, м');
title('Зависимость смещения от времени')
Результаты работы системы MatLab
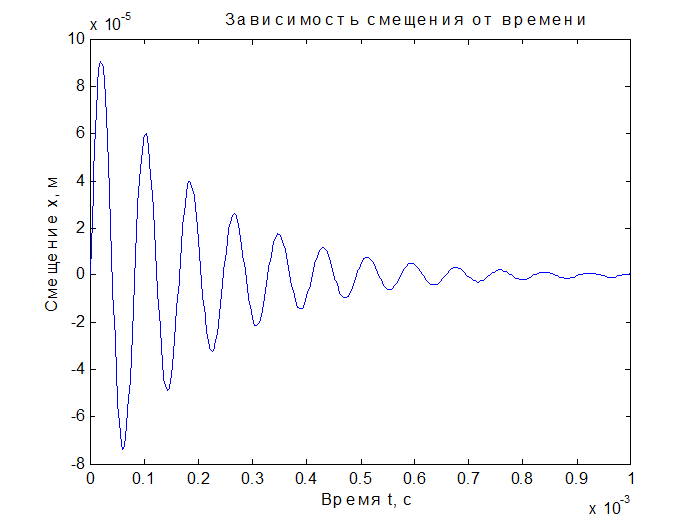 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.