Высокомолекулярные соединения. Методы определения средней молекулярной массы полимеров

Вероятность того, что длина цепи лежит между R и R+dR равна:

W(R)dR = (3/2πNl2)3/2exp(-3R2/2Nl2)4πR2dR

Функция распределения W(R) определяется таким образом, что

∫ от 0, до∞ W(R)dR=1

В этом случае среднеквадратичное расстояние между концами цепи

<R²> = ∫ от 0, до∞  R²W(R)dR

<R²>=N^1l2

Вывод R ~ N^1/2 правомерен для идеальной цепи с любым механизмом гибкости (а не только для модели свободно-сочлененной цепи).

Модель с фиксированным валентным углом

Рассмотрим модель с фиксированным валентным углом Θ между сегментами длиной b и свободным внутренним вращением [U(ϕ) = 0] (Рис. 4).

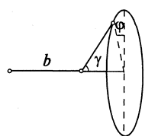 Такая модель близка к реальной цепи с поворотно-изомерным механизмом гибкости.

Используя те же самые обозначения, можно записать для данного случая, так же как для свободно- сочлененной цепи

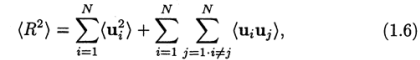
как и прежде <u_i²> = b², но теперь величина <u_iu_j> для i≠j не обязательно равна нулю: < u_iu_j >=b²<cosθ_ij>, где θ_ij — угол между сегментами i и j. Поэтому

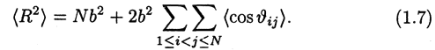
Чтобы вычислить величину <cosθ_ji> рассмотрим сначала простейший случай, когда i и j —

соседние сегменты. Ясно, что при этом <cosθ_i,_i+1>=cosγ.

Для вычисления среднего угла между сегментами i и i+2 разложим вектор u_i+2 на две компоненты: параллельную и перпендикулярную вектору u_i+1 (Рис. 5).

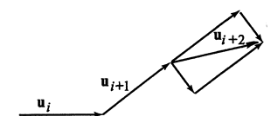
Ясно, что при вращении сегмента i+2 относительно сегмента i+1 среднее значение перпендикулярной проекции будет равно нулю, а среднее значение параллельной проекции есть cosγ. При поворотах сегмента i+1 относительно сегмента i для среднего значения проекции ui+2,i на направление вектора ui возникает еще один фактор cosγ. Таким образом, <cosθ_i,i+2>=(cosγ)². Пользуясь теми же рассуждениями, получим в общем случае

Таким образом, из уравнений (1.7) и (1.8) получаем

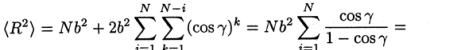
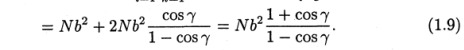
Во второй части уравнения (1.9) использовалась формула

∑(от К=1 до ∞)a ^к = a/ 1-a

и предположение о том, что величина N–i достаточно велика, так что при суммировании ее можно заменить бесконечностью.

Для модели с фиксированным валентным углом

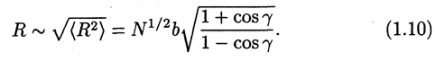
Видно, что усредненные размеры цепи по-прежнему пропорциональны N1/2, т.е. и в этой модели цепи клубок находится в запутанной конформации.

Эффект заторможенного вращения

Уравнения, выведенные в предыдущем разделе, основаны на гипотезе о свободном вращении полимерной цепи вокруг связей. В действительности вращение вокруг ординарных связей обычно ограничено (заторможено). При условии постоянства валентного угла θ, достаточных длине и гибкости цепи и постоянстве плотности вероятности внутренних углов вращения ϕ среднеквадратичное расстояние между концами цепи принимает вид

< R² >= Nl²(1- cos θ/1+ cos θ)*(1+ <cos φ>/1-<cos φ>)

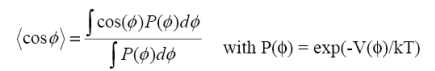
вероятность поворота на угол φ

Сравнение этого соотношения с предыдущим показывает, что ограничения гибкости цепи не приводят к изменению типичной зависимости расстояния между концами цепи от квадратного корня из числа звеньев цепи, а лишь изменяет эффективную длину звена цепи. На самом деле это общее свойство идеальной полимерной цепи независимо от модели.

Общее идеальное выражение зависимости R от длины цепи. Зависимость расстояния между концами цепи от квадратного корня из числа звеньев цепи сохраняется даже при введении конформационных корреляций. Кун в своей классической работе указал, что такое соотношение должно соблюдаться почти всегда для достаточно длинных цепей даже в том случае, если ограничения гибкости цепи не могут быть проанализированы во всех деталях. Исходя из этого, он предложил заменить реальную цепь с фиксированными валентными углами и различными ограничениями вращению вокруг связей, соединяющих атомы главной цепи, "эквивалентной цепью", имеющей ту же контурную длину и состоящую из меньшего числа Zo "статистических элементов цепи", которые, однако, соединены свободно без ограничения валентных углов. Значение bo подбирается таким образом, чтобы среднеквадратичное расстояние между концами эквивалентной цепи было равно среднеквадратичному расстоянию