Аппроксимирующая функция, построение графика с нанесением экспериментальной точки

Задание 3

            Пусть функция  задана следующей таблицей:

          Используя метод наименьших квадратов, аппроксимировать ее полиномом первой степени: . Построить график аппроксимирующей функции  и нанести на этот же график экспериментальные точки. Сравнить полученные коэффициенты полинома с коэффицициентами полученыыми с помощью функции polyfit.

          Указание:для определения коэффициентов полинома использовать следующую систему линейных уравнений

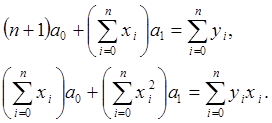
          Решение системы уравнений вида

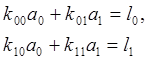
относительно неизвестных величин a_j  и параметров k_ij, l_i можно представить  в матричном виде

.

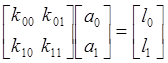          Задавая элементы матрицы K, столбца L, неизвестные элементы столбца A можно определить с помощью команды A = K \ L.

          Пример. Пусть требуется решить систему уравнений

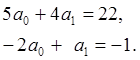
          В Matlab записываем следующую последовательность команд:

K = [5,4; -2,1];

L = [22; -1];

A = K \ L

Получаем ответ:

A =

     2

     3

          Очевидно, таким образом можно решить системы из многих линейных уравнений.