Моделирование процесса динамического нагружения образца горной породы с использованием символьного пакета расширения Symbolic Math Toolbox

Работа №2. Моделирование процесса динамического нагружения образца горной породы с использованием символьного пакета расширения Symbolic Math Toolbox.

I. Цель работы:

Научиться составлять уравнение движения для взаимодействующих тел, определять начальные условия и получать решение уравнения с помощью символьного пакета расширения MatLab Symbolic Math Toolbox.

II. Задание и порядок выполнения

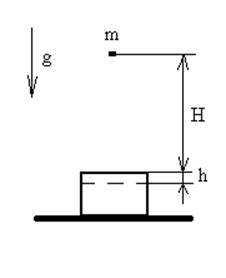
Образец горной породы, положенный на несжимаемое основание, испытывает динамическое нагружение несжимаемым грузом, падающим без начальной скорости с высоты H. При этом происходит упругая деформация образца только в направлении падения груза на величину h. Определить продолжительность динамического нагружения T.

            В соответствии со вторым законом Ньютона , где k – коэффициент жесткости породы получим дифференциальное уравнение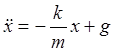, решением которого будет некоторая функция времени – x(t), содержащая две постоянные C₁ и C₂. Эти постоянные можно определить из начальных условий  (скорость груза в момент касания с породой) и x(0) (перемещение породы в момент касания). Из графика x(t) можно определить величину T. Время T можно также вывести из аналитического рассмотрения функции x(t). Принять x = 0,1 мм, H = 3 м.

При решении задания следует использовать функцию dsolve в следующем виде dsolve(‘D2x = -(k/m) * x – g’, ‘Dx(0) = sqrt(2*g*H)’, ‘x(0) = 0’). В качестве аргументов функция принимает 3 символьных строки: запись дифференциального уравнения, начальное условие по скорости, начальное условие по перемещению.

III. Пример оформления

>>dsolve('D2x=-(k/m)*x+g', 'Dx(0)=sqrt(2*g*H)', 'x(0)=0')

ans =

(g*m+1/2*m*(-g*(-m*k)^(1/2)+2^(1/2)*(g*H)^(1/2)*k)/(-m*k)^(1/2)*exp(1/m*(-m*k)^(1/2)*t)-1/2*m*(g*(-m*k)^(1/2)+2^(1/2)*(g*H)^(1/2)*k)/(-m*k)^(1/2)*exp(-1/m*(-m*k)^(1/2)*t))/k

>> t=0:1e-4:1e-3;

>> x=(g*m+1/2*m*(-g*(-m*k)^(1/2)+2^(1/2)*(g*H)^(1/2)*k)/(-m*k)^(1/2)*exp(1/m*(-m*k)^(1/2)*t)-1/2*m*(g*(-m*k)^(1/2)+2^(1/2)*(g*H)^(1/2)*k)/(-m*k)^(1/2)*exp(-1/m*(-m*k)^(1/2)*t))/k;

>> plot(t,x)

Warning: Imaginary parts of complex X and/or Y arguments ignored.

>> xlabel('Время t, c')

>> ylabel('Смещение x, м')

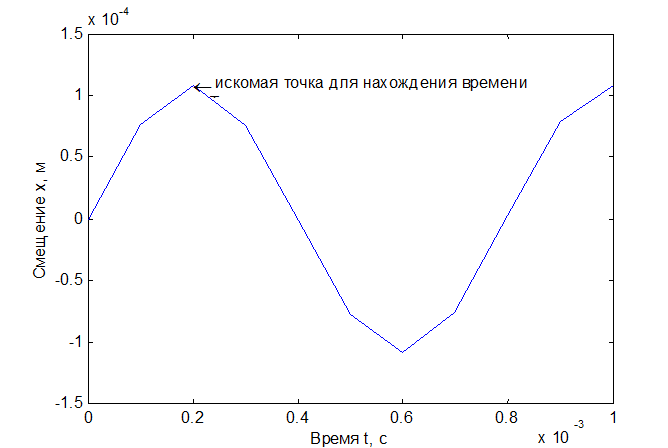>> text(0.2e-3, 1.1e-4, '\leftarrow искомая точка для нахождения времени T')