




























Государственное образовательное учреждение
высшего профессионального образования
“петербургский государственный университет путей сообщения”
Кафедра высшей математики
Методические указания для студентов заочного факультета
по выполнению курсовой работы
по дисциплине “ВЫСШАЯ МАТЕМАТИКА”
Раздел «ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
Санкт Петербург
2005
Специфической особенностью деятельности специалиста железнодорожного транспорта является работа в условиях наличия постоянно изменяющейся информации в виде экспериментальных (производственных, опытных или измерительных) показателей (статистических данных). Анализ такой информации с целью принятия конкретных решений требует применения методов математической статистики. Статистические методы широко используются при решении многих практических задач железнодорожного транспорта.
Поэтому освоение методов статистической обработки результатов практики эксплуатации железнодорожной техники (результатов производственной деятельности, натурных испытаний, эксперимента, измерений и т.п.) является одной из важных задач обучения студентов в ПГУПС.
Курсовая работа в разделе «Теория вероятностей и математическая статистика» дисциплины «Высшая математика» направлена на привитие у студентов начальных навыков решать следующие практические задачи:
- обрабатывать и анализировать результаты практики эксплуатации железнодорожной техники и формулировать правильные выводы;
- оценивать точность и надежность сформулированных выводов;
- обобщать результаты обработки в виде таблиц и графиков и сравнивать их с теоретическими положениями.
Методические указания разработаны с учетом первого опыта проведения курсовых работ по указанному разделу в Университете. Оно предназначено для студентов, обучающихся на заочном факультете, по специальностям «В», «Лт», «ЭТ» и «АТС».
В пособии изложены общие требования по выполнению курсовой работы, включая подготовку, проведение и анализ расчетов, а также по оформлению расчетно-пояснительной записки и защите работы.
Теория вероятностей
1. Предмет теории вероятностей. Испытания и события. Классификация событий. Операции над событиями Пространство элементарных событий. Алгебра событий .
2. Понятие случайного события. Относительная частота событий и ее свойства. Устойчивость относительных частот. Статистическое определение вероятности.
3. Классическое и геометрическое определение вероятности. Понятие об аксиоматическом построении теории вероятностей .
4. Условная вероятность. Независимые события. Теорема умножения вероятностей. Теорема сложения вероятностей Формула полной вероятности. Формула Байеса.
5. Схема Бернулли. Формула Бернулли. Локальная и интегральная теоремы Лапласа. Теорема Пуассона.
6. Дискретные случайные величины. Законы распределения. Примеры. Математическое ожидание и дисперсия дискретной случайной величины. Биноминальный закон распределения. Закон Пуассона.
7. Непрерывные случайные величины. Функция распределения, плотность распределения, их взаимосвязь и свойства. Примеры. Математическое ожидание и дисперсия непрерывной случайной величины, их свойства. Начальные и центральные моменты распределения случайной величины. Равномерное и показательное распределения и их свойства .
8. Нормальный закон распределения. Вероятностный смысл параметров нормального распределения. Вероятность попадания нормально распределенной величины в заданный интервал. Правило трех сигм.
9. Сходимость по вероятности. Неравенство Чебышева. Закон больших чисел в форме Чебышева. Закон больших чисел для схемы Бернулли. Центральная предельная теорема Ляпунова. Условие Ляпунова. Интегральная теорема Лапласа - частный случай центральной предельной теоремы.
Основные понятия математической статистики
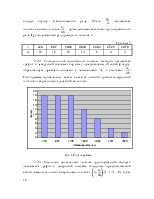
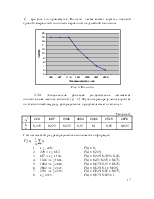
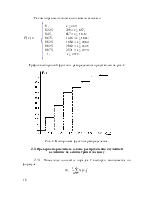
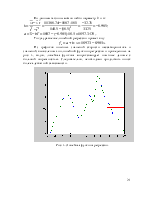
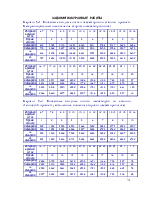
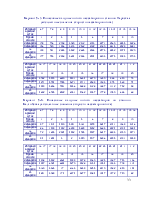
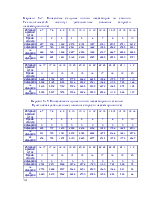
1. Генеральная совокупность и выборка. Вариационный ряд. Гистограмма. Эмпирическая функция распределения, выборочные средняя и дисперсия .
2. Статистическая оценка параметров распределения. Точечные оценки параметров генеральной совокупности. Принцип выбора точечных оценок (состоятельность, несмещенность, эффективность). Точечная оценка математического ожидания. Точечная оценка дисперсии.
3. Интервальная оценка параметров генеральной совокупности. Доверительная вероятность и доверительный интервал. Доверительный интервал для математического ожидания. Определение необходимого объема выборки .
3. Статистическая проверка гипотез. Понятие о критериях согласия. Критерий согласия Пирсона .
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Чистяков В.П. Курс теории вероятностей. - М.: Наука, 1982.
2. Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: Высшая школа, 1977.
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статике. - М.: Высшая школа, 1979.
4. Кальницкий Л.А. и др. Специальный курс высшей математики для вузов. - М.: Высшая школа, 1976 .
5. Кухаренко Л.А. Теория вероятности. Методические указания. Часть 1. - СПб: 1984.
6. Кухаренко Л.А. Теория вероятности. Методические указания. Часть 2. - СПб: 1984.
7. Математическая статистика , статистическое оценивание параметров по методу максимального правдоподобия , статистическая проверка гипотез. Методические указания. - СПб: 1990.
8. Кухаренко Л.А., Родин В.И., Телятников А.Е. Математическая статистика. Методические указания к лабораторной работе. - Спб: 1988.
9.Клепикова Л.С., Кузьмина М.В., Кухаренко Л.А. Статистическая проверка гипотез. Методические указания. - Спб: 1984.
1. Дайте классическое определение вероятности. В чем состоит различие между вероятностью и относительной частотой?
2. Дайте определение условной вероятности. Какие события называются независимыми?
3. Дайте определение произведения событий. Сформулируйте теоремы умножения для зависимых и независимых событий.
4. Какие события называются несовместными? Сформулируйте теоремы сложения для совместных и несовместных событий.
5. Напишите формулу Бернулли. Когда эта формула применяется?
6. Приведите примеры дискретных и непрерывных случайных величин.
7. Дайте определение функции распределения и плотности распределения вероятностей непрерывной случайной величины.
8. Напишите формулы для математического ожидания и дисперсии случайной величины.
9. Нарисуйте график плотности вероятности нормально распределенной случайной величины. Как меняется график при изменении параметров а и s?
10. Как построить гистограмму?
11. Какая разница между точечной и интервальной оценками параметра?
Целью курсовой работы является отработка студентами навыков использования основных статистических методов для овладения первичными навыками обработки опытных данных, которые широко используются при решении практических задач в повседневной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.