Примечание: МВ, Мр – молярные массы растворенного вещества и растворителя соответственно; r - плотность раствора.
1.2.1. ГАЗОВЫЕ СМЕСИ.
Газовые смеси получают непосредственным смешиванием специально подобранных газов в нужных соотношениях. Нередко смеси газов образуются в результате химического взаимодействия веществ, находящихся в ином агрегатном состоянии.
Идеальные газы
В достаточном для практики приближении свойства многих реальных газов можно принять подобными свойствам идеальных газов. Поэтому В кинетической теории газов постулируется модель идеального газа, основанная на следующих приближениях:
- Молекулы газа являются материальными точками, обладающими некоторой массой и размерами ничтожно малыми по сравнению с расстоянием между отдельными молекулами.
- Молекулы находятся в состоянии непрерывного и беспорядочного движения, равновероятного во всех направлениях[ii].
- Скорости движения отдельных молекул могут меняться в пределах от 0 до ¥.
- Молекулы не взаимодействуют между собой и при соударении ведут себя как упругие шары.
Таким образом, идеальный газ можно представить как некоторое предельное состояние реального газа, находящегося при бесконечно малом давлении. Примером идеального газа может служить разреженный газ в вакууме или газ в космическом пространстве.
В смеси идеальных газов каждый газ отличается только своей химической природой, но не поведением. Это означает, что каждый газ характеризуется собственным давлением, называемым парциальным давлением. Парциальное давление газа численно равно тому давлению, которое имел бы данный газ, если бы он один занимал весь объем.
В соответствии с законом Дальтона «наблюдаемое давление смеси идеальных газов (pобщ) равно сумме парциальных давлений отдельных газов (рi)». Это означает, что:
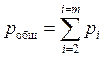 (1.2)
(1.2)
где m - число различных газов, составляющих смесь.
Следует отметить, что смесь идеальных газов подчиняется уравнению Клапейрона – Менделеева. Поэтому для любого компонента смеси выполняется равенство:
рiV=niRT (1.3)
где: ni – количество компонента i в молях; R = 8,314 Дж/(К×моль) - молярная газовая постоянная[iii]; р – давление газа, Па; V - объем, м3; Т – температура, выраженная в шкале Кельвина Т= t oС + 273..
Уравнение (1.3) часто называют уравнением состояния идеального газа и с этим названием связывают определение идеального газа[iv].
Реальные газы
Понятие идеальный газ, безусловно, является одним из центральных в химической термодинамике (см. главу 2) поскольку позволяет существенно упростить многие термодинамические расчеты. Однако в ряде случаев при описании реальных газов оно оказывается недостаточным.
Наиболее простым уравнением состояния реального газа, которое учитывает отклонение свойств реального газа от свойств идеального газа при сравнительно невысоких давлениях является уравнение Ван-дер- Ваальса:
(p + n2 a/VМ2)(v - b) = nRT (1.4)
где: n – количество молей газа, aи b – постоянные, характеризующие объем отделной молекулы газа (постоянная b) и поправку на взаимное притяжение между молекулами,
1.2.2. ДИСПЕРСНЫЕ СИСТЕМЫ
Дисперсные системы, представляют собой смеси различных веществ, находящихся в различных агрегатных состояниях. В дисперсных системах выделяют дисперсную фазу и дисперсионную среду. Вещество дисперсной фазы и дисперсионной среды может находится в различных агрегатных состояниях. Это определяет конкретные характеристики дисперсной системы и позволяет классифицировать дисперсные системы (см табл. 1.4).
Т а б л и ц а 1.4
Классификация дисперсных систем по агрегатному состоянию дисперсной фазы и дисперсионной среды
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.