2. Метод эквивалентного генератора (МЭГ).
Метод основан на теореме Гельмгольца – Тевенена и используется для определения тока в выбранной ветви сложной цепи.
Теорема Гельмгольца – Тевенена (об активном двухполюснике).
 |
а б
Рис. 6
Согласно этой теореме, любая линейная цепь (активный двухполюсник) относительно выбранных зажимов может быть представлена ветвью (рис. 6) с последовательным соединением эквивалентного источника ЭДС - EЭГ и эквивалентным (входным) сопротивлением - RЭГ.
EЭГ – ЭДС генератора равна напряжению, возникающему на разорванных зажимах выбранной ветви, (EЭГ =UXX12 холостой ход генератора).
RЭГ – сопротивление генератора определяется как входное сопротивление схемы (RЭГ = RВХ12) относительно зажимов выбранной ветви. При расчете входного сопротивления ЭДС и ток источников тока полагаются равными нулю, а в схеме остаются внутренние сопротивления источников (для идеального источника ЭДС – RE = 0, а источника тока – RJ = ∞).
Если активный двухполюсник (рис.6,а), к которой присоединена ветвь c резистором RH к зажимам 1 и 2, заменить источником с ЭДС – EЭГ и сопротивлением – RЭГ (рис.6,б), то ток IH в присоединённой ветви не изменится.
Порядок расчёта (МЭГ):
1. Определение ЭДС эквивалентного генератора:
в исследуемой ветви принимается положительное направление тока, ветвь размыкается и по направлению тока вводится напряжение UXX;
для простейшего контура с участием UXX по второму закону Кирхгофа составляется уравнение. Вошедшие в него токи обозначают индексом «Х», например, - IXN;
при разомкнутой ветви любым методом находятся токи, вошедшие в уравнение;
подставив их в уравнение, получают UXX = ЕЭГ.
2. Отыскание сопротивление эквивалентного генератора RЭГ:
в оставшейся части цепи исключаются источники, и заменяются их внутренними сопротивлениями RE = 0, RJ = ¥;
в случае необходимости преобразовывается схема и записывается её входное сопротивление относительно разомкнутой ветви: RВХ = RЭГ.
|
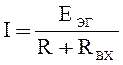 (3)
(3)
Задача 4
Решение
1. Выделим узлы, к которым присоединена ветвь с резистором R5 (узлы 2 и 5), и зададим положительное направление искомого тока I5. (схема рис. 12):
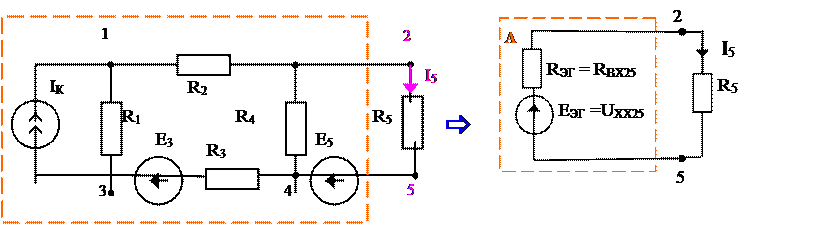 |
Рис. 13
2. Относительно выделенных зажимов 2 и 5 цепь представим эквивалентным генератором рис. 13.
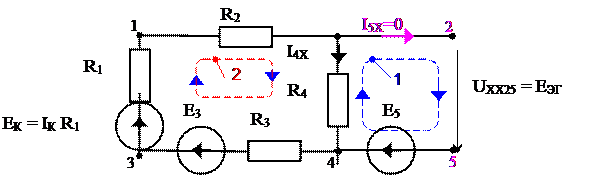 |
Рис. 14
3. Определим ЭДС эквивалентного генератора (расчётная схема рис. 14):
ветвь с искомым током размыкаем и по направлению тока вводим напряжение EЭГ = UXX25;
для контура, в который входит напряжение UXX25, составляем уравнение по второму закону Кирхгофа для контура 1, вошедшие в него токи обозначают индексом «Х»;
UXX25 – I4Х R4 = E5; (11)
для определения токов, вошедших в уравнение (11) преобразуем источник тока в источник ЭДС EК = IК R1 = 110 В, ток I4Х определи по второму закону Кирхгофа, составленному для контура 2;
I4Х (R1 + R2 + R3+ + R4 ) = EК + E3;
I4Х = 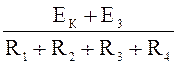 =
= 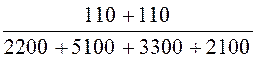 = 0.0173 А.
= 0.0173 А.
подставив их в уравнение (11), определим:
UXX25 = ЕЭГ =E5+ I4Х R4 = 127 + 0.0173 2100 = 163.4 В.
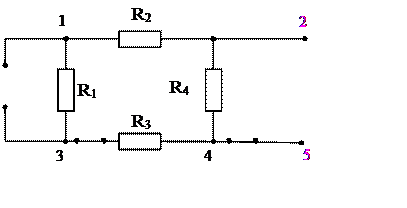 4.
Определение сопротивления эквивалентного генератора RЭГ (расчётная
схема рис. 15):
4.
Определение сопротивления эквивалентного генератора RЭГ (расчётная
схема рис. 15):
Рис. 15
в цепи рис 14 исключаем источники, и заменяем их внутренними сопротивлениями RE = 0, RIk = ¥, поученная схема приведена на рис. 15;
рассчитаем входное сопротивление цепи относительно зажимов 2 - 5:
RВХ25 = RЭГ = 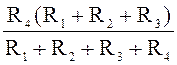 =
= 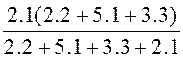 =
1.753 кОм.
=
1.753 кОм.
5. Искомый ток находится по закону Ома:
I5 = 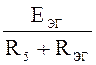 =
= 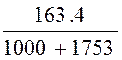 0.0593
А.
0.0593
А.
Ответ: I5 = 59.3 мА.
Задача 5
 |
|||
|
|||
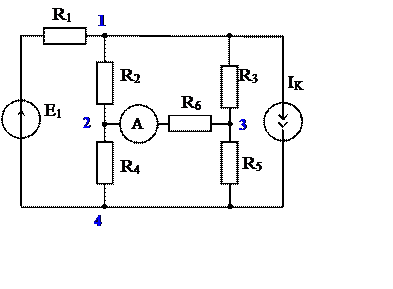
Рис. 16
Решение
 1. Выделим узлы, к которым присоединена
ветвь с резистором R6 (узлы 2 и 3), и
зададим положительное
направление искомого тока в амперметре - I6. (схема
рис. 17).
1. Выделим узлы, к которым присоединена
ветвь с резистором R6 (узлы 2 и 3), и
зададим положительное
направление искомого тока в амперметре - I6. (схема
рис. 17).
 |
|||
|
|||
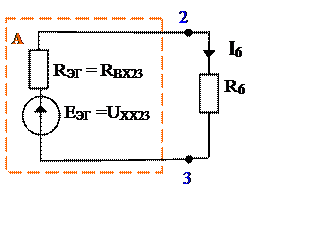
Рис. 17
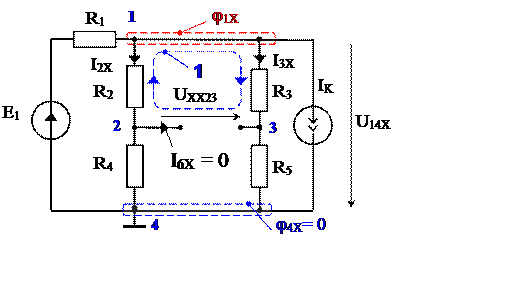
2. Относительно выделенных зажимов 2 и 3 цепь представим эквивалентным генератором.
 |
![]() Рис.
18
Рис.
18
3. Определим ЭДС эквивалентного генератора (расчётная схема рис. 18):
ветвь с искомым током размыкаем и по направлению тока вводим напряжение EЭГ = UXX23
для контура, в который входит напряжение UXX25, составляем уравнение по второму закону Кирхгофа для контура 1, вошедшие в него токи обозначают
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.