Алгоритм численного решения системы интегральных уравнений галленовского типа, структурная схема программы, страница 2

Указанные достоинства уравнения Мея определяют его широкое применение при анализе директорных, спиральных, и многих других видов излучателей.

Рассмотрим некоторые виды базисных функций. В соответствии с идеей прекционных методов, токи на проводнике представляются в виде разложений по системе базисных линейно независимых функций , :

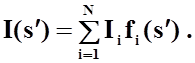
Базисные функции должны обеспечивать:

 быструю сходимость численного решения;

 хорошую обусловленность матрицы системы линейных алгебраических уравнений;

 быстрое и точное вычисление матричных элементов системы линейных алгебраических уравнений.

В настоящее время отсутствует критерий, по которому можно заранее определить пригодность данного базиса в конкретной задаче, и этот вопрос решается путем машинного эксперимента.

Базисные функции, используемые при решении интегральных уравнений для тонких проводников, делятся на два класса: базис полной области и кусочный базис ( базис подобластей ). К первому классу относятся базисные функции, каждая из которых определена на всем проводнике длиной L . В случае базиса подобластей проводник делится на отрезки, на каждом из которых определяется базисная функция, отличающаяся от соседних сдвигом. В ряде случаев соседние подобласти взаимно перекрываются для того чтобы лучше аппроксимировать непрерывное распределение тока.

Примеры базисных функций полной области:

-  разложение в ряд Фурье по тригонометрическим функциям:

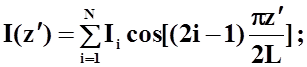
-  полиномиальное разложение Б. Д. Поповича:

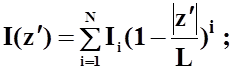
-  трехчленная аппроксимация Р. В. П. Кинга:

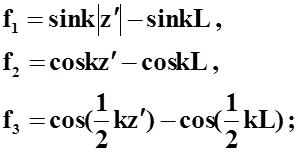
Примеры базисных функций подобластей:

-  кусочно-постоянная функция:

     

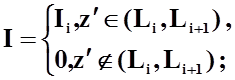
-  кусочно-линейные функции:

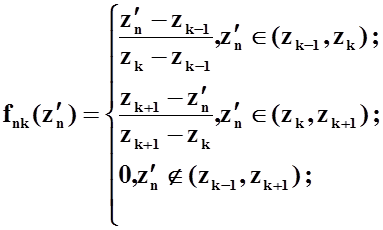
-  кусочно-синусоидальные функции:

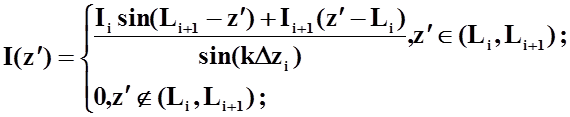
где - размер i-ого отрезка, заключенного между точками разбиения проводника.

Базисные функции полной области были исследованы в [4]. Результат гласит, что для уравнений Галлена, решаемых методом коллокации, при длине плеча вибратора  , для получения достаточной точности необходимо удерживать около 20 членов Фурье, в то время как при полиномиальном разложении или трехчленной аппроксимации достаточно 3-4 членов для обеспечения высокой точности решения. Это объясняется тем, что эти функции отражают характерные особенности действительного распределения тока, в частности, быстрое его изменение в близи возбуждающего зазора для антенн не резонансной длинны, поведение тока на концах вибратора.

Полиномиальное разложение и трехчленная аппроксимация являются непригодными для сегментов, не имеющих свободных концов, так как базисные функции здесь обращаются в нуль, то есть в точках . Удобной модификацией разложения Поповича, пригодного для антенн, состоящих из отрезков прямолинейных проводников, является разложение вида:

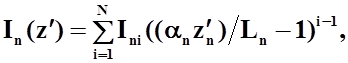
где постоянные вещественные коэффициенты  могут быть определены из численного эксперимента при решении модельных задач.

Базис подобластей широко исследован для уравнений Поклингтона и Мея ( Галлена ). Он универсален и широко используется для решения разнообразных задач. При решении уравнения Поклингтона, используя кусочно-синусоидальный базис, появляется возможность не проводить сложного двойного интегрирования, так как поля, создаваемые отдельными сегментами, могут быть найдены в аналитической форме.

Выбор кусочно-линейного базиса, помимо его простоты, обеспечивает получение быстрого и устойчивого процесса сходимости численного решения, приводит к системе линейных алгебраических уравнений с лучшей обусловленностью по сравнению с другими видами базисных функций. При анализе структур, имеющих соединения проводников, использование базиса подобластей дает автоматическое выполнение правила Киргоффа для токов в узлах.

Итак, при анализе проволочных антенн, в том числе сложной конфигурации, определенными преимуществами обладают интегральные уравнения Мея, а в случае прямолинейных проводников – интегральные уравнения Галлена. Это вытекает из следующих особенностей:

 уравнение успешно решается экономным в вычислительном плане методом коллокации;

 хорошая сходимость решения наблюдается практически независимо от вида базисных функций;

 правая часть уравнения представляет собой кусочно-гладкую функцию даже при сосредоточенном возбуждении ( модель возбуждающего источника – дельта-генератор ).

В качестве недостатка интегральных уравнений Мея можно отметить наличие операций интегрирования в ядре, но выше было показано, как эту операцию можно исключить.

3.3.3 Структурная схема программы расчета электродинамических параметров тонкопроволочных антенн.

Структура универсальной программы автоматизированного расчета тонкопроволочных антенн представлена на рис.7.

Программа состоит из следующих модулей: программы подготовки и редактирования данных «edit.exe»; программы расчета распределения токов по элементам антенны «sol.exe»; программы расчета электродинамических характеристик антенны «res.exe».

Управляющая программа «men.exe» позволяет обратиться к любому из модулей и осуществлять необходимый обмен данными между ними.

Редактор исходных данных «edit.exe» предназначен для подготовки входных данных, необходимых при расчете. Он позволяет:

 создавать новые наборы данных и редактировать уже созданные;

 записывать вновь созданные и отредактированные наборы данных в библиотеку на жесткий или гибкий магнитные диски;

 считывать из библиотеки уже существующие наборы данных для их использования в расчетах или редактирования.