Оптимизация параметров методами дифференцирования и Гаусса-Зейделя

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Владимирский Государственный Университет

Кафедра КТРЭС

Лабораторная работа №6

«Оптимизация параметров                                      методами дифференцирования и Гаусса-Зейделя»

Выполнил:

студент группы РЭ-104

Проверил:

Владимир 2006
Цель работы: ознакомится с методами дифференцирования и Гаусса-Зайделя поиска оптимума и изучение свойств этих методов.

Исходные данные:

, начальная точка x₁₀= x₂₀=-2,  шаг Dx₁= Dx₂=1.

Метод дифференцирования

Для нахождения экстремума функции составим и решим систему, содержащую частные производные целевой функции по параметрам x₁ и x₂:     

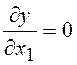
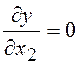
   4-0,2x₂-0,4x₁=0

6-0,2x₁-1,2x₂=0

   x₁=8,18

x₂=3,64

В точке с координатами x₁  и x₂ максимум функции, т.к.

,

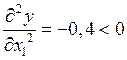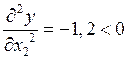
Подставив значения x₁ и x₂ в исходное уравнение, получаем y=30,27272.

Метод Гаусса-Зайделя

Начальная точка x₁₀= x₂₀=-2,  шаг Dx₁= Dx₂=1.

          Экстремум, найденный по методу Гаусса-Зейделя, находится в точке с координатами x₁=8, x₂=4;  при этом y=30,2.

Вывод: в ходе выполнения лабораторной работы был найден эстремум функции  двумя методами: дифференцирования и Гаусса-Зейделя. Координаты точки экстремума, найденные обоими методами, незначительно различаются.

Методом дифференцирования (точным методом) было получено:

x₁=8,18

x₂=3,64

y=30,27272.

Методом Гаусса-Зейделя (приближенным методом) получено:

x₁=8

x₂=4

y=30,2.

Таким образом, методом Гаусса-Зейделя дал приближенный результат с точностью, равной заданному шагу.