Самым распространённым элементом радиотехнических схем, является колебательный контур, образованный параллельным соединением индуктивности и ёмкости.
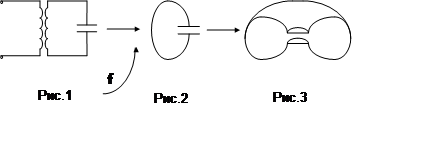 |
Недостаток контура низкая добротность, связанная с уменьшением энергии электромагнитного поля в такой системе с увеличением активных потерь обусловленных поверхностным эффектом и с потерями на излучение.
Возрастает запасенная энергия, уменьшаются потери. В таких объемных резонаторах сохранены конструктивные особенности присущие системам с сосредоточенными параметрами (можно выделить L и C).
С ростом частоты, L и C уменьшаются, и в пределе получают контур как на Рис.2. Он вырождается в утилитарную конструкцию, в которой роль ёмкости играют две металлические пластины, а роль индуктивности – проводник соединяющий их. Это характерное преобразование для волн сантиметрового диапазона. Добротность таких контуров достаточно низка. Причина этого в следующем, малая величина LC элементов, приводит к снижению энергии, запасённой в таком контуре.
Вследствие поверхностного эффекта, увеличиваются
потери в проводниках. ![]() . Сильно возрастают потери на
излучении. Возможен следующий путь увеличения добротности на ВЧ. Как показано
на Рис.2, вследствие параллельного соединения элементов, увеличивается
резонансная частота.
. Сильно возрастают потери на
излучении. Возможен следующий путь увеличения добротности на ВЧ. Как показано
на Рис.2, вследствие параллельного соединения элементов, увеличивается
резонансная частота.
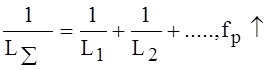
Отсюда мы получим конструкцию как на Рис.3. Получим локальный объём, ограниченный локальными стенками.
Колебательная система, ограничивающая себя проводящими, локальными стенками называют объёмным резонатором.
Этот подход обладает недостатками, которые присущи колебательным системам с сосредоточенными параметрами.
С ростом частоты, объём колебательной системы
уменьшается ![]() , снижается добротность. Сростом
частоты возрастают технологические трудности реализации подобных систем.
, снижается добротность. Сростом
частоты возрастают технологические трудности реализации подобных систем.
Рассмотрим более прогрессивный способ реализации подобных систем, с использованием структур с распределёнными параметрами. Рассмотрим реализацию колебательной системы из отрезков линии передач.
Рассмотрим КЗ двухпроводную линию.
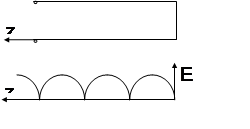
В такой линии режим КЗ.
Режим КЗ, будет повторятся в точках, которым удовлетворяют следующие соотношения.
![]() ,
, ![]()
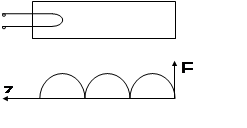

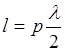
В частности, если взять линию КЗ с двух сторон, то как показано в курсе ОТЦ, в ней будет колебательный процесс. Причём, его частные параметры:
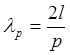
Характерная особенность таких колебательных систем, что они могут резонировать на множестве частот. Вдоль такой колебательной системы, должно укладываться целое число полуволн.
Мы рассмотрели колебательную систему на примере отрезка двухпроводной линии. Также, подобные системы могут быть реализованы на любых линиях передач, в том числе и на волноводах.
Характерные особенности, будут заключатся, в следующем:
Стоячая волна может возникать по всем трём координатам, внутри резонатора. Подобные резонаторы будут резонировать на кратных частотах, вследствие явления дисперсии.
1. частотная дисперсия
2. стоячие волны 3-м координатам
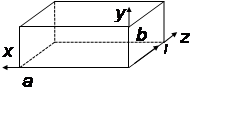 Берём стандартный, прямоугольный
волновод, с волной
Берём стандартный, прямоугольный
волновод, с волной ![]() .
.
Рассмотрим прямоугольный волновод сечением ![]() .
.
Определим структуру поля и параметры электромагнитных колебаний, возникающих в таком резонаторе.
H10:
z=0 z=l
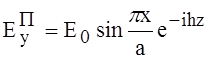
![]()
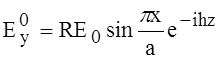
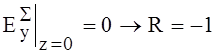
При наличии КЗ, в стенке появится отражённая волна.
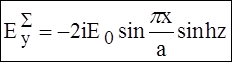
По определению, продольно-волновое число ![]() . Для его определения воспользуемся
граничной задачей.
. Для его определения воспользуемся
граничной задачей.
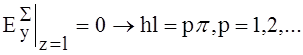
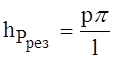
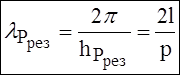
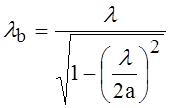 ; учитывая это, можно
написать:
; учитывая это, можно
написать: 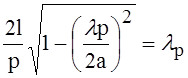
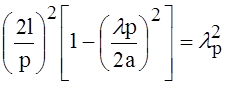
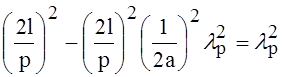
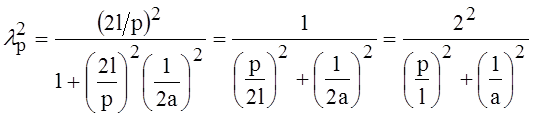
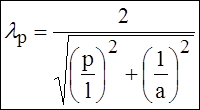 - длина волны
резонансная, в свободном пространстве.
- длина волны
резонансная, в свободном пространстве.
Индекс “p”, имеет простой физический смысл. Он показывает, число стоячих полуволн, вдоль оси резонатора.
Рассматриваемый тип колебаний, имеет следующую
абривеатуру ![]() .
.
До образования резонатора, в волноводе, существовала
волна ![]() .
.
![]() - в таком резонаторе
одна полуволна.
- в таком резонаторе
одна полуволна.
Тип колебаний:
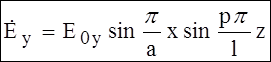 – так обозначим “y” компоненту.
– так обозначим “y” компоненту.
![]() =>
=> 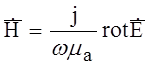
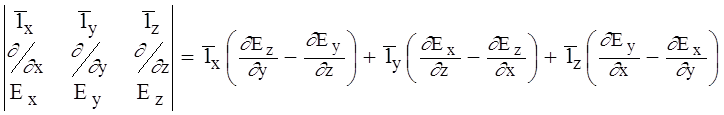
имеется только y-составляющая.
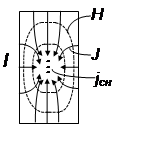
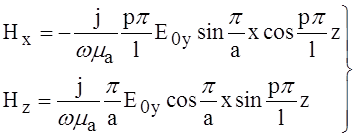
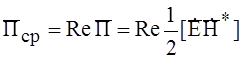 ;
; ![]() – Это означает, что в резонаторе
отсутствует распространение энергии, но существует колебательный процесс, в
результате которого энергия дважды за период превращается из электрической в
магнитную и наоборот.
– Это означает, что в резонаторе
отсутствует распространение энергии, но существует колебательный процесс, в
результате которого энергия дважды за период превращается из электрической в
магнитную и наоборот.
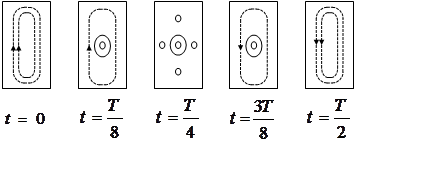 t=0 – поле
только магнитное;
t=0 – поле
только магнитное;
t=T/8 – магнитное поле убывает и электрическое поле возрастает;
t=2T/8 – поле только электрическое.
 Определить совокупность резонансных
частот всех возможных типов колебаний, существующих в прямоугольном резонаторе
с размерами
Определить совокупность резонансных
частот всех возможных типов колебаний, существующих в прямоугольном резонаторе
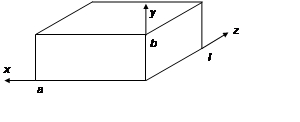
с размерами ![]() . Введём декартову систему координат, при
этом пусть размер l совпадает с осью Z.
. Введём декартову систему координат, при
этом пусть размер l совпадает с осью Z.
Пусть в поперечном сечении с размерами ![]() структура поля совпадает со структурой
поля волны
структура поля совпадает со структурой
поля волны ![]() . Резонансная длина волны, связана с длиной
волны в волноводе с размерами
. Резонансная длина волны, связана с длиной
волны в волноводе с размерами ![]() дисперсионным
уравнением.
дисперсионным
уравнением.
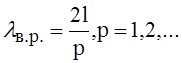
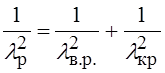
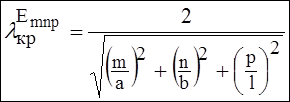 (1)
(1)
Пологая если структура колебания в поперечном сечении резонатора
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.