Усилительные клистроны. Двухрезонаторный усилительный клистрон, страница 2

Обозначим фазу напряжения между сетками резонатора в момент пролета электроном плоскости первой сетки через Q₁, а фазу напряжения, соответствующую пролету электрона через вторую сетку – Q₂. Тогда среднее значение переменного напряжения, воздействующего на электрон в течение времени его пролета между сетками модулятора, определится выражением:

                  _Q2         

u_ср = 1/(Q₂ - Q₁) ò U_1m sin Q dQ,                                    (2)

                      ^Q1                                                                                                                        

где Q = wt – фаза переменного напряжения в момент пролета электрона через середину резонатора. Полагая угол пролета электрона через зазор модулятора равным Q₃=wt_з=wd_з/V₀, где t_з - время пролета, d_з - зазор,  получим:

u_ср= (sin (Q₃ /2)/Q₃/2) U_1m sin Q .                                  

Величина b₁=(sin(Q₃/2))/Q₃/2 называется коэффициентом взаимодействия электронов с полем резонатора. Коэффициент  b₁ = 1 при  Q₃  = 0  обращается в нуль, когда электрон находится в пространстве резонатора в течении всего периода переменного напряжения. В клистронах угол пролета Q₃ лежит в пределах от p/2 до p. При этом  b₁ » 0.9 ¸0.6.

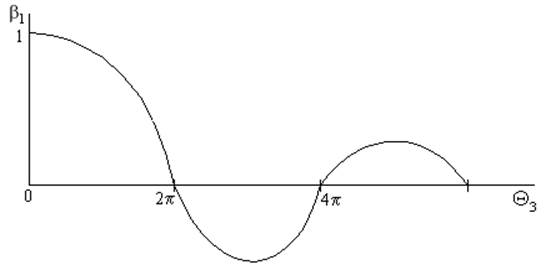
Рис. 3

Величина M = b₁ U_1m/(2U₀) называется коэффициентом модуляции скорости электронного потока.Величина X = MQ₀, где Q₀ - угол пролета электроном от середины зазора модулятора до плоскости z,не изменившим своей скорости, называется  параметром группирования.

Величина X характеризует эффективность группирования.  Она определяется произведением коэффициента модуляции скорости и угла пролета. X тем выше, чем больше амплитуда СВЧ напряжения, пространство дрейфа, угол пролета и меньше ускоряющее напряжение.

 Изменение плотности тока    

Угол пролета электроном некоторого расстояния изменяется в зависимости от момента его прихода в зазор модулятора:

Q_д = Q_x – Q = Q₀ – X sin Q.                                             

Параметр группирования X определяется амплитудой переменной составляющей электронного тока. Из рис. 4 видно, что в общем случае конвекционный ток электронов не синусоидальный. Он богат высшими гармониками. Откуда следует, что на базе пролетного клистрона легко построить умножитель частоты.

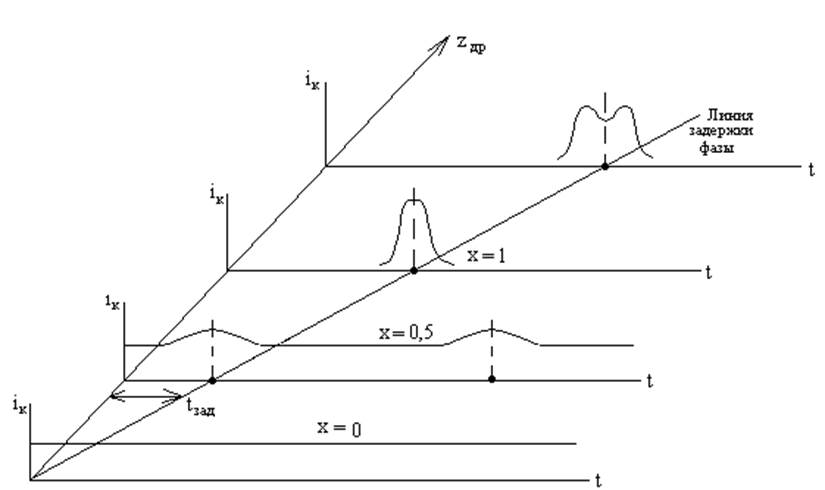
Рис. 4

Амплитуды гармоник:      I_n=2I₀J_n(nX),                                                   

где    I₀ - ток катода    (постоянная составляющая) клистрона;

J_n(nX)- функция Бесселя 1-го рода n-го порядка от аргумента nX. Для 1-ой гармоники J_1max (X) достигается при X=1.84   J₁ (1.84) = 0.58. Для второй гармоники оптимальное значение при Х=1.55. Вторая гармоника при этом будет составлять 83% от первой (0.58х0.83). Десятая гармоника максимальна при Х=1.2, а ее амплитуда равна половине первой гармоники. Графики функций Бесселя приведены на рис. 5.

Если бы ток был в виде d-импульса, то при полном группировании электронов I_1max= 2I₀ (вместо 0.58  коэффициент 2).

В выходном резонаторе наведенный ток определяется коэффициентом взаимодействия электронов с полем  выходного резонатора М₂ и амплитудой соответствующей гармоники тока электрона :        I_1нав.= I₁M_2,                                                                                      

где                                    M₂ = (sin (Q_3вых./ 2))/(Q_3вых./ 2).                                      

Для эффективного взаимодействия электронов с полем необходимо уменьшить угол пролета и выбирать оптимальный режим по группированию.

Параметры и характеристики двухрезонаторного пролетного клистрона       

1. Выходная мощность - мощность сигнала заданной гармоники, которая зависит от амплитуды наведенного тока в резонаторе, ускоряющего напряжения U₀, настройки входного и выходного резонаторов и от входной     мощности P_{в х}. Для первой гармоники : P_1max=0.58 P₀, где P₀ = I ₀U₀ - мощность постоянного тока иона не зависит от P_вх всех клистронов. График выходной мощности пролетного клистрона приведен на рис.6.