


Квантовая механика
Согласно гипотизе Луи де Бройля не только части эл.маг.
излучения но и любые другие движущ. Мкрочастици присущие карпускулярно волновой
дуализм, Следовательно состояние микрообъекта можно описывать с помощью
волнового уравнения которым является уравнение Шредингера. Пусть движ. Микро
частиц соответствует плоская волна.![]() .
. ![]()
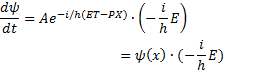
![]()
![]() )
)
![]()
![]()
Если частица
движется в силовом поле а следственно обладает потенциальностью энергии то
взаимосвязь энергии и импульса ![]() +u.В трёх мерном пространстве
ур.Шредингера запишется в:
+u.В трёх мерном пространстве
ур.Шредингера запишется в:
![]() Тогда ур. Шрёдингера
имеет вид:
Тогда ур. Шрёдингера
имеет вид: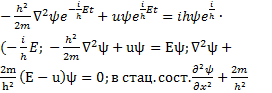 (E-u)
(E-u)![]()
Ур.Шрёдиегира
имеет решение если на волновую функцию накладываются ограничения непрерывности
однозначности и конечности.Согласно гипотизе длину волны объекта можно найти
так же как и взаимосвязь импульса фотона и длины волны излучения.![]() если скорость частици волна то не обходимо учитывать релятивийский
эффект изменения массы
если скорость частици волна то не обходимо учитывать релятивийский
эффект изменения массы ![]()
Соотношение не определенностей
Отличительной особенностью механики микромира от механики микрообъектов явл. То что для микрообъектов невозможно абсалютно точно задать значение динамически сопряженных величин.
Принцип неопределеномтей:
Произведение
неопределенностей динамически сопряженных величин не может быть меньше по
величине постоянной планка. Если одна из величин стремиться к определенности то
неопределенность другой величины к бесконечности. К соотношению неопред. Можно
придти исходя из следующ. Соображений. Пусть пучек электронов падает на
пластиеку имеющюю щель размером х перпендикулярно уё повкрхности.После
прохождении пластинки пучёк электронов дифрагировал в пределах темесного угла
от 0 до фи.![]()
Потенциальная яма
Потенциальной
ямой называют обл. промтранства в которой потенциал энергии частици равна 0 так
как потенциал. Яма бесконечно глубокая то вероятность окружения частици за
пределами ямы равна 0.Тогда ур. Шредингера выглядит: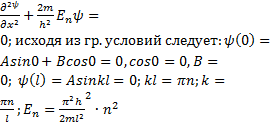
Для
нахождения пораметра используют условие нормировки 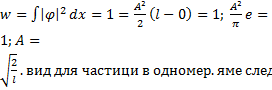 x)=
x)=![]() sin
sin![]() x.
x.
Прохождение частици сквозь потенциальный барьер.
Пусть частица движется в положттельном направлении х и на своём пути встречает барьер шириной l и высотой
Тогда ур. Шрёдингера для 1и3 запишется:
1,3: ![]() +
+![]() +
+![]() (
(![]()
Решение: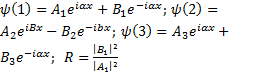
Вероятность
прохождения частици сквозь барьер определяется коэффициентом прозрачности
потенциального барьера Д ![]() Коэф. Потенц. Барьера в прямоуг. Форме :
Коэф. Потенц. Барьера в прямоуг. Форме :![]()
Явление прохождения частици сквозь потенциальный барьер при условии что энергия частици меньше высоты потенц. Барьера назыв. Туннельным эффектом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.