Движение материальной точки с тангенциальным ускорением. Решение задачи

№ 1.14

Условие: Материальная точка движется по окружности радиусом R. Её тангенциальное ускорение изменяется по закону W_τ=kt, k>0. В какой момент времени t с начала движение модули нормального и тангенциального ускорения будут равны? Чему равно полное ускорение материальной точки в этот момент времени? Какой угловой путь φ пройдёт точка к этому моменту времени? Качественно изобразите закон изменения угловой скорости w как функцию времени.

Дано: R, Wτ=kt, k>0 Wτ=Wн

Найти: t, Wп ,φ; Построить график w(t)

Решение:

Как известно, тангенциальное ускорение характеризует изменение вектора скорости по модулю с течением времени:

 

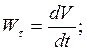
Следовательно, модуль скорости можно найти, проинтегрировав формулу тангенциального ускорения:

Однако по условию нам дано, что тангенциальное ускорение изменяется по закону W_τ=kt, причём k>0:

k – величина постоянная и её можно вынести за знак интеграла:

 

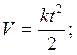
Мы знаем, что в данный момент времени t модуль тангенциального ускорения равен модулю нормального:

 (1)

Нормальное ускорение характеризует изменение вектора скорости по направлению и находится как:

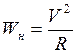 - подставляя эту формулу в уравнение (1), получаем:

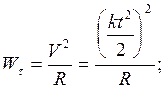
Но в то же время, W_τ=kt

Следовательно,

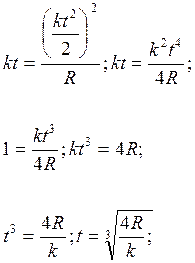
Теперь, когда известен момент времени t, мы можем найти полное ускорение материальной точки в этот момент времени.

Полное ускорение точки можно найти как:

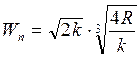
Найдём угловой путь φ, который пройдёт точка к моменту времениt.

По условию задачи W_τ=kt, но в то же время, W_τ=εR. Следовательно,

.

Угловое ускорение 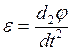. Выразим отсюда путь φ:

.

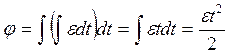Следовательно,

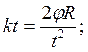
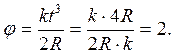
Закон изменения угловой скорости w как функции времени.

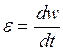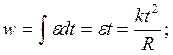;График функции 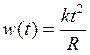 будет выглядеть как парабола, сжатая по оси Оу на величину , если 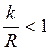 и растянутая, если на величину , если 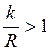 (по сравнению с графиком ).

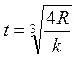Ответ: момент времени , полное ускорение материальной точки в этот момент времени 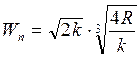, угловой путь рад.

№ 1.17

Условие: Тело брошено сначала под углом α₁ к горизонту со скоростью V₁ , а затем под углом α₂ со скоростью V₂ (α₁> α₂). В начальный момент времени V_1x=V_2x. Сравнить в указанных случаях радиусы кривизны траектории в высшей точке подъёма тела. Построить качественно зависимость проекции импульса p_1y и p_2y как функцию времени движения тела. Сопротивления движению нет.

Дано: α1, α2,  α1> α2, V1x=V2x

Найти: Построить графики p1y (t) и  p2y (t)

Решение:

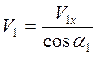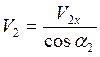; . Так как cos(α₁)>cos(α₂), то .

По теореме Пифагора . Исходя из того, что  и  V_1x=V_2x ,.

Тело в обоих случаях достигает максимально высокой точки за одинаковый промежуток времени t_a так как  V_1x=V_2x.

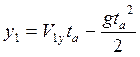 и .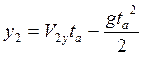

Но y₁ и y₂ можно заменить на R₁ и R₂ соответственно. Следовательно,

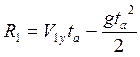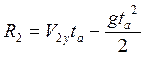 и . Если t_a=const, g=const и , то R₁>R₂.

Проекцию импульса данной точки на ось Оу можно найти следующим образом:  - для 1-го случая и  - для 2-го случая.

На графике:

t_a и t_b  - время в наивысшей точке траектории и на момент приземления соответственно; p_1y и p_2y – импульсы тела в первом и втором случаях соответственно.

Ответ: Радиус кривизны в высшей точке подъёма в первом случае больше, чем во втором.

№ 1.36

Условие: На обод маховика диаметром  намотан шнур D=60 см, к концу которого привязан груз массой m=2,0 кг. Определить момент инерции маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t=3,0 с приобрёл угловую скорость w=9,0 рад/с.

Дано: D=60 см, m=2,0 кг, t=3,0, w=9,0 рад/с

Найти: I=?

Решение:

Согласно уравнению динамики вращательного движения, .

Момент силы в данном случае можно найти как .

На маховик в данном случае действует только сила тяжести .

Величина ε – угловое ускорение – постоянно, так как сила, действующая на маховик, не изменяется.

.

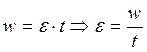Окончательно, подставляя все вышеописанные выражения в уравнение динамики вращательного движения, получаем:

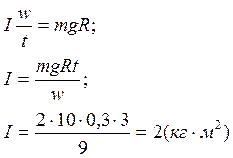
Ответ: момент инерции маховика равен 2 кг·м².

№ 1.57

Условие: В цилиндр массой m₁=3 кг и радиусом R=10 см, покоящийся на плоскости, попадает пуля массой m₂=9 г, летящая со скоростью V₀=60 м/с. Пуля летит параллельно плоскости цилиндра на высоте от неё и перпендикулярно образующей цилиндра. Считая удар абсолютно неупругим, найдите линейную скорость оси цилиндра, угловую скорость цилиндра. Проскальзыванием цилиндра пренебречь.

Дано: m1=3 кг, R=10 см=0,1 м, m2=9 г=0,009 кг, V0=60 м/с,  h=0,12 м

Найти: V, w

Решение:

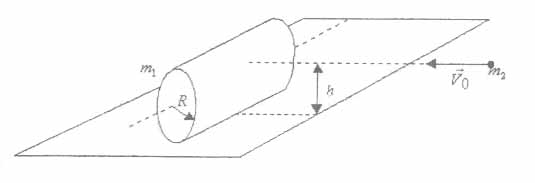
По теореме Штейнера найдём момент инерции относительно любой точки на поверхности цилиндра:

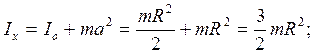где a – расстояние от оси вращения (на рисунке - О) цилиндра до поверхности, равное его радиусу R,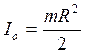 - момент инерции цилиндра относительно оси О.

Так как данную систему можно считать изолированной, то в ней выполняется закон сохранения момента импульса: момент импульса замкнутой системы частиц остаётся постоянным: , где L₁ – момент импульса системы до взаимодействия (момент импульса летящей пули), а L₂ – момент импульса системы после взаимодействия (момент импульса катящегося цилиндра).

Момент импульса пули: ;

Момент импульса цилиндра: 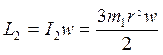 (масса пули пренебрежимо мала по сравнению с массой цилиндра, поэтому её можно не учитывать при движении цилиндра после того, как пуля врезалась в него);

Найдём угловую скорость вращения цилиндра:

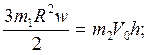
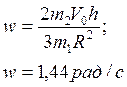
Найдём линейную скорость оси цилиндра:

Предположим, что цилиндр совершил один оборот во время качения. Тогда путь S, который от прокатился, будет равен . В то же время, угловую скорость за один оборот можно найти как: 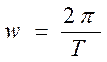, где Т – период вращения тела.

Линейная скорость оси цилиндра 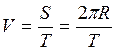. В то же время, . Следовательно, .

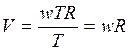V=0,14 рад/с.

Ответ: Линейная скорость оси цилиндра равна 0,14 рад/с,  угловая скорость вращения цилиндра равна 1,4 рад/с.

№ 1.70

Условие: Определить периметр Р квадрата со стороной а, движущегося со скоростью 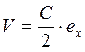, вдоль одной из своих сторон, где С – скорость света.

Дано: а,

Найти: Р

Решение:

При движении тела с релятивистскими скоростями его длина уменьшается относительно стороннего наблюдателя (системы координат) согласно формуле .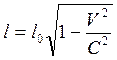

В данном случае, l₀ есть сторона квадрата а, сжимающаяся до размера l.

.

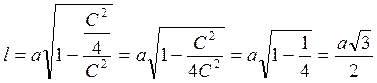Периметр квадрата .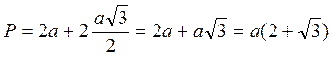

Ответ: Периметр квадрата равен .