Анализ эквивалентности технологических процессов

Федеральное агентство по образованию РФ

Государственное образовательное учреждение высшего профессионального образования

"Владимирский государственный университет"

Кафедра КТРЭС

Лабораторная работа № 2

Анализ эквивалентности технологических процессов

Вариант № 16

Выполнил: ст.гр. Р-107

Проверил:

Владимир, 2010

Цель работы: Изучение  методов сравнения эквивалентности технологических процессов, происходящих на различных производственных линиях.

Исходные данные.

Ряд 1: , , .

Ряд 2: , , .

Ряд 3: , , .

Объем выборки n = 50.

Ход работы.

Доверительный  интервал  для  математического  ожидания     находится    по    неравенству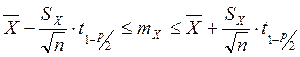,где   ,  - среднее арифметическое и стандартное отклонение в выборке;  - объем выборки (задается  преподавателем);  - уровень  значимости;  - квантиль  распределения  Стьюдента,  определяемый  по     уровню  значимости    и  числу   степеней   свободы. Из формулы видно, что доверительный интервал для математического ожидания получается симметричным.

Подставляя числа можно легко рассчитать доверительный интервал для математического ожидания для каждого ряда причем при различных доверительных вероятностях. Пусть это будут следующие вероятности: ,  и . Результаты расчета сведены в таблицу 1.

Таблица 1 – Расчет доверительных интервалов при различных вероятностях

На рис. 1 представлена зависимость ширины интервала для математического ожидания от доверительной вероятности.

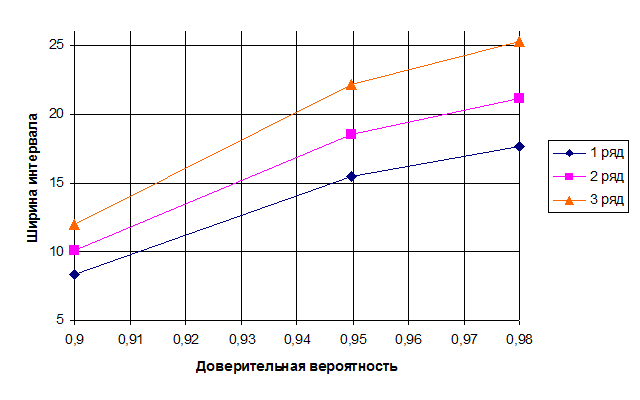
Рис. 1. Зависимость ширины интервала от доверительной вероятности

Доверительный  интервал  для  дисперсии    при  нормальном  законе  распределения  равен

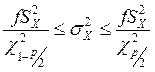, где   - выборочная  дисперсия;

,  - квантили распределения Пирсона, определяемые по уровню значимости  и числу степеней свободы .

Результаты расчета доверительного интервала для дисперсии сведены в таблицу 2.

Таблица 2 – Расчет доверительных интервалов для дисперсии

На рис. 2 представлена зависимость ширины интервала для дисперсии от доверительной вероятности.

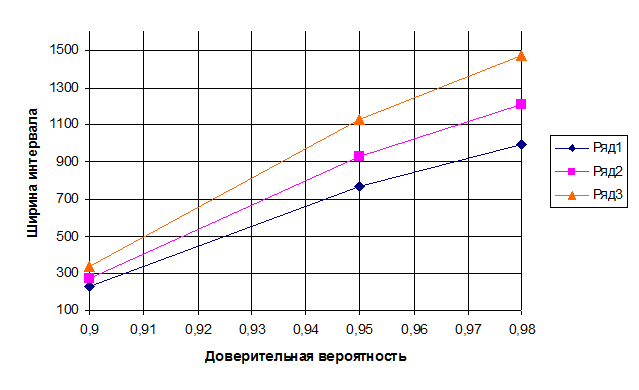
Рис. 2. Зависимость ширины доверительного интервала для дисперсии

от доверительной вероятности

В  качестве  критерия  значимости   для  сравнения  двух  дисперсий   обычно  используется  критерий  Фишера.  Две  дисперсии  считаются  равными  с  доверительной  вероятностью  ,   если  выполняется  неравенство