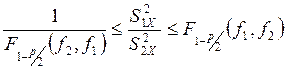Физика \ Управление качеством электронных средств

Анализ эквивалентности технологических процессов, страница 2

- квантили распределения Фишера, определяемые в зависимости от уровня значимости р и чисел степеней свободы; — объемы выборок.

Результаты расчета неравенства с использованием критерия Фишера сведены в таблице 3.

Таблица 3 – Проверка однородности дисперсии

γ	1 и 2 ряды			2 и 3 ряды			1 и 3 ряды
γ	1/F		F	1/F		F	1/F		F
0,9	0,685942	0,294969	1,457849	0,685942	0,766678	1,457849	0,685942	0,226147	1,457849
0,95	0,615856	0,294969	1,623755	0,615856	0,766678	1,623755	0,615856	0,226147	1,623755
0,98	0,545053	0,294969	1,834685	0,545053	0,766678	1,834685	0,545053	0,226147	1,834685

По таблице 3 видно, что неравенство соблюдается не для всех рядов. При доверительной вероятности 0,9 дисперсии для 1-го и 3-го рядов однородными считать нельзя.

Генеральные математические ожидания считаются равными, если выполняется неравенство

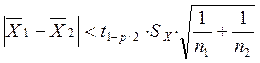Средневзвешенная дисперсия

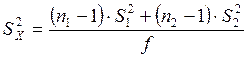, где — число степеней свободы.

Результаты проверки однородности математических ожиданий приведены в таблице 4.

Таблица 4 – Проверка однородности математического ожидания

γ	1 и 2 ряды				2 и 3 ряды				1 и 3 ряды
γ			\|m₁_x-m₂_x\|	Т			\|m₂_x-m₃_x\|	Т			\|m₁_x-m₃_x\|	Т
0,9	26,17	1,677	50,6	8,78	34,91	1,677	1,12	11,71	29,08	1,677	51,72	9,76
0,95		2,011		10,5		2,011		14,05		2,011		11,7
0,98		2,408		12,6		2,408		16,81		2,408		14,01

Как видно из таблицы 4, не все пары математических ожиданий можно считать однородными.

Вывод: В ходе выполнения лабораторной работы были рассчитаны доверительные интервалы для математического ожидания и дисперсии при различных доверительных вероятностях (табл. 1, 2). Как видно из построенных зависимостей (рис. 1, 2) ширина интервала зависит от доверительной вероятности. Т.е. с чем большей надежностью требуется гарантировать полученный результат, тем в большем диапазоне значений он может находиться.

С помощью критерия Фишера была проверена однородность дисперсий (табл. 3). Как оказалось, все пары дисперсий можно считать однородными, кроме дисперсий для 1-го и 3-го рядов при доверительной вероятности . Однородность математических ожиданий проверялась с помощью критерия Стьюдента (табл. 4). Оказалось, что не все пары математических ожиданий можно считать равными. Например, для 1, 2 и 1, 3 рядов при доверительной вероятности их нельзя считать равными.

При производстве однотипной продукции на нескольких параллельных линиях часто требуется знать, является ли отличие в математических ожиданиях или дисперсиях случайностью или имеет место нарушение техпроцесса. Для этого проводят проверку на однородность с помощью различных критериев (Фишера, Кохрена и др.). Если рассматриваемые величины не являются однородными, то это говорит о каких-либо нарушениях в техпроцессе, его нестабильности.

1 2

Скачать файл