Задание на РГР:
p0=-6; p1=-0.1; p2=-0.2; p3=-1+j0.5; p4=-1-j0.5; p5=0; K=100
По заданным нулю и пяти полюсам передаточной функции разомкнутой системы записать выражение для:
1) Передаточной функции разомкнутой системы
2) Передаточной функции замкнутой системы
3) Дифференциальное уравнение системы
4) Составить и нарисовать структурную схему замкнутой системы
Найти:
1) АЧХ разомкнутой системы
2) ФЧХ разомкнутой системы
3) АФХ разомкнутой системы
4) Переходную характеристику разомкнутой системы
5) Весовую функцию разомкнутой системы
6) ЛАЧХ и ЛФЧХ
7) Построить асимптотическую ЛАЧХ и ЛФЧХ
Проанализировать устойчивость системы:
1) Методом Райвиса-Гурвица
2) Методом Михайлова
3) Методом Найквиста.
4) По ЛАЧХ и ЛФЧХ
5) Определить запасы устойчивости по амплитуде и фазе в случае устойчивой системы
6) Дать рекомендации по изменению структурной схемы в случае неустойчивой системы.
Решение:
1) Передаточная функция разомкнутой системы:
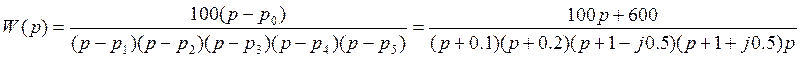
2) Передаточная функция замкнутой системы:
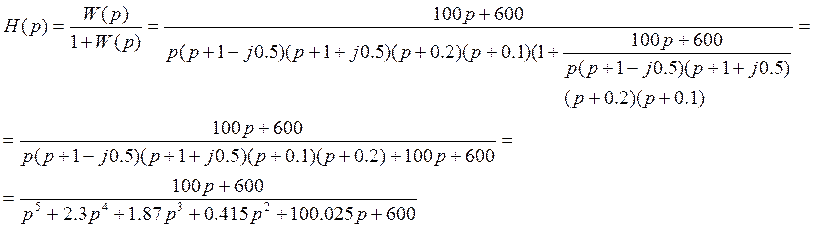 3) Дифференциальное уравнение
системы:
3) Дифференциальное уравнение
системы:
В дифференциальной форме передаточную функцию системы можно
записать в следующем виде: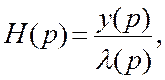 т.е. отношение реакции
цепи на воздействие к этому воздействию.
т.е. отношение реакции
цепи на воздействие к этому воздействию.
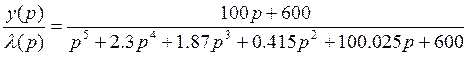
![]()
Учитывая 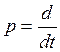 , получаем
дифференциальное уравнение цепи:
, получаем
дифференциальное уравнение цепи:
![]()
4. Структуру замкнутой системы можно представить в виде разомкнутой системы, охваченной ООС. Разомкнутую систему можно представить в виде включенных последовательно звеньев:
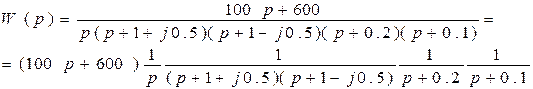 ;
;
Значит структурная схема имеет вид:

5) АЧХ разомкнутой системы:
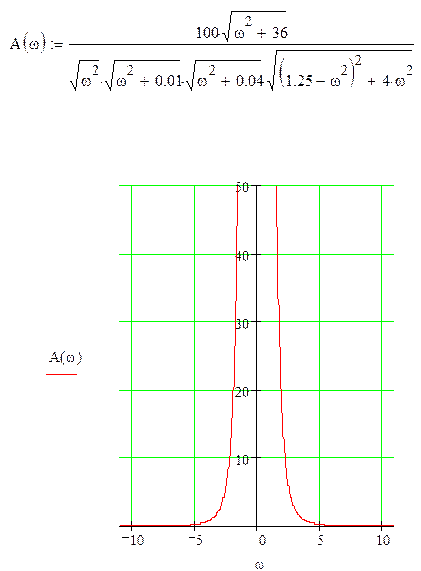
6) ФЧХ разомкнутой системы:
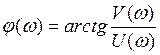

7) АФХ разомкнутой системы:
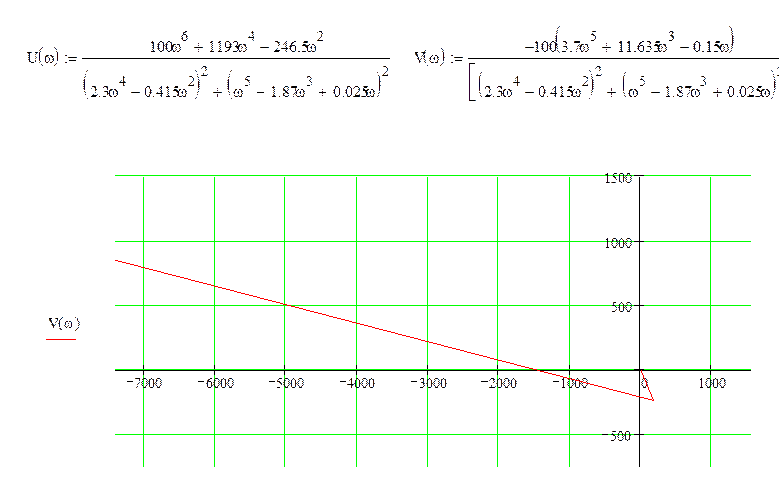
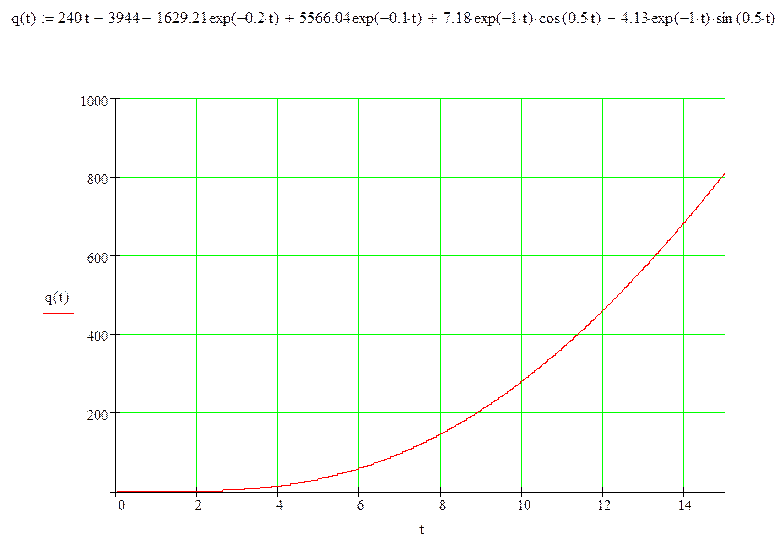
8) Переходная характеристика разомкнутой системы:
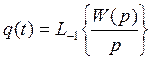
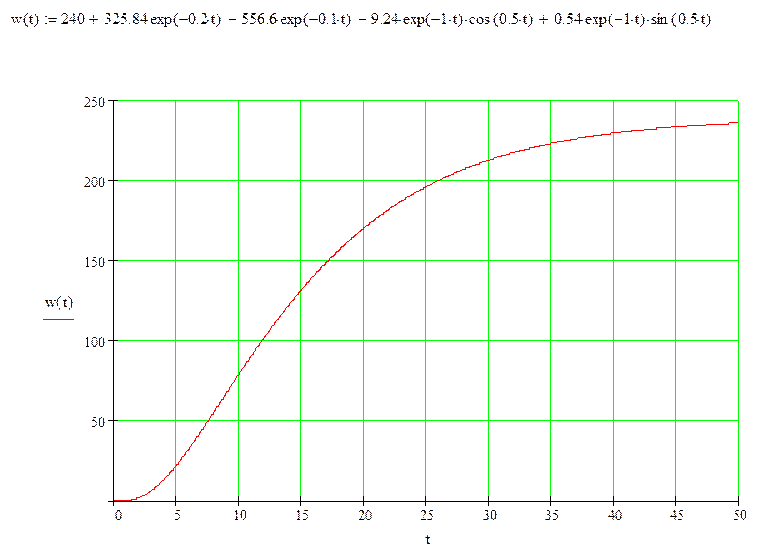
9) Весовая функция:
![]()
10) ЛАЧХ и ЛФЧХ:
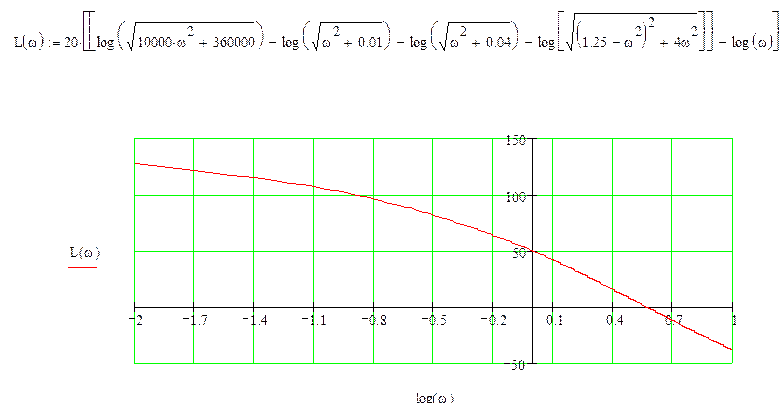 ЛФЧХ:
ЛФЧХ:
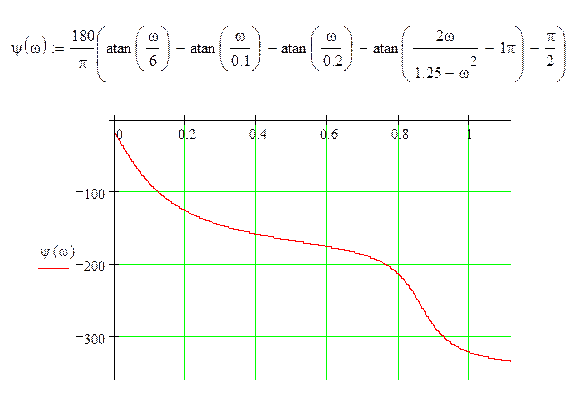
11) Асимптотическая ЛАЧХ:
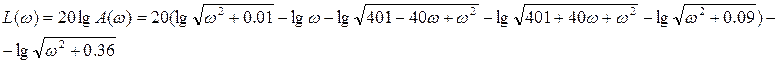
12)Оценка устойчивости методом Рауса-Гурвица:
![]()
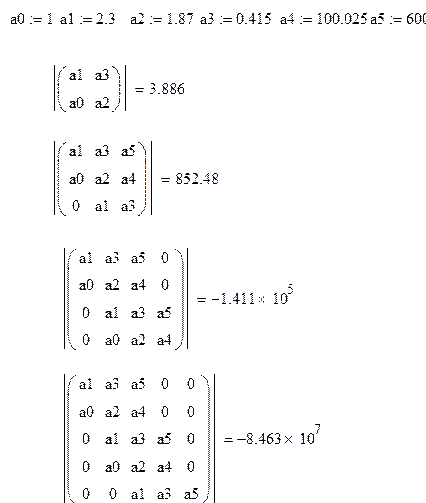
Для того чтобы система была устойчива необходимо и достаточно,
чтобы все gi были
больше нуля и ![]() . Следовательно, данная система
неустойчива.
. Следовательно, данная система
неустойчива.
13) Оценка устойчивости методом Михайлова.
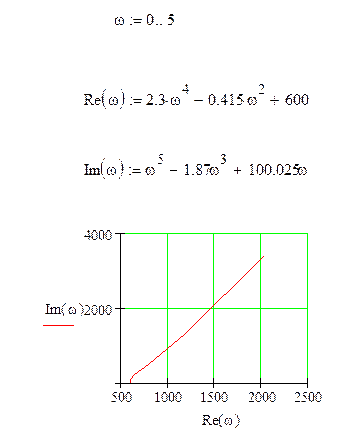
Как мы видим годограф Михайлова не обходит последовательно все четверти следовательно система неустойчива.
14) Оценка устойчивости методом Найквиста:
Построим АФХ системы:
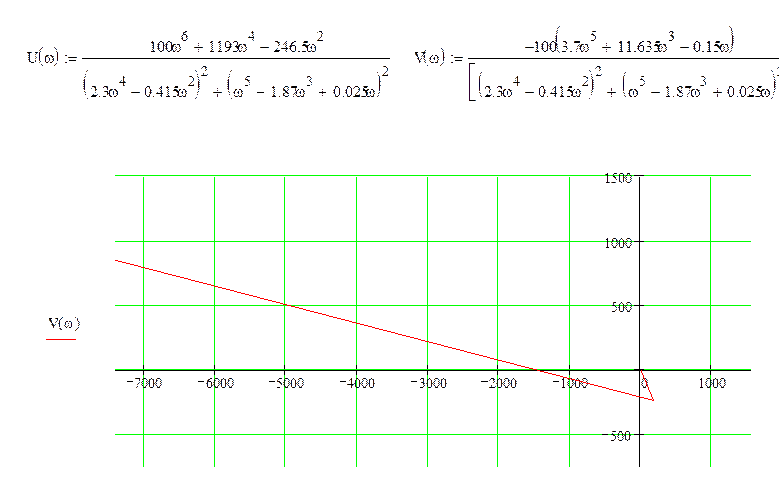
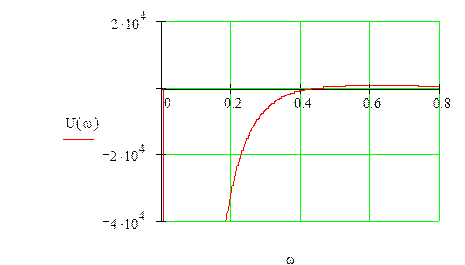
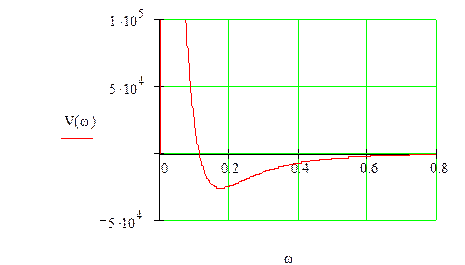
Посмотрим, охватывает ли АФХ точку (-1:j0). Так как при положительном переборе частот от 0 до бесконечности обход идет против часовой стрелки, следовательно, внутренняя область от оси, следовательно, точка (-1;j0) попадает в контур, следовательно, система неустойчива.
15) Оценка устойчивости по ЛАЧХ и ЛФЧХ.
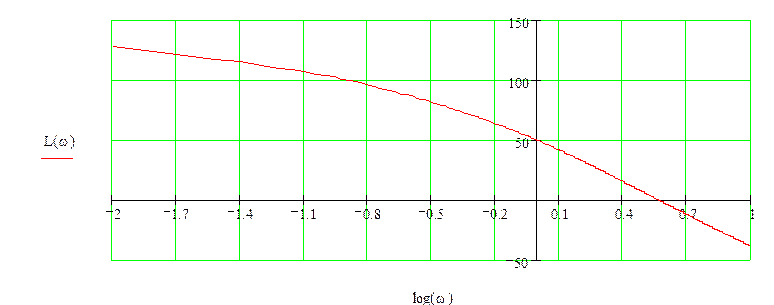
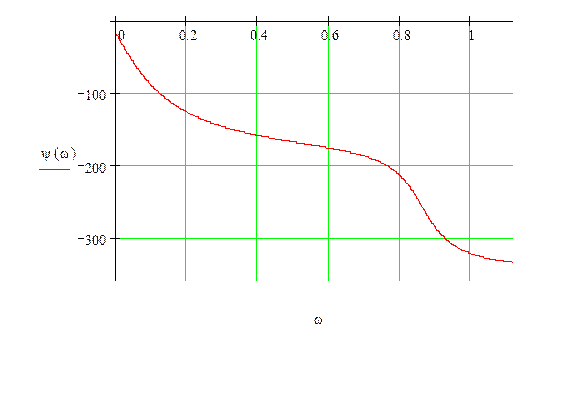
Сопоставляя график ЛАЧХ и ЛФЧХ видим, что при L(A(ω))>0 не
происходит положительных переходов. Следовательно, система не устойчива. ![]()
16) Для того чтобы система стала устойчивой необходимо изменить передаточную характеристику системы. Для повышения устойчивости уберем из цепи интегратор, значение нуля увеличим до -0.1 и уменьшим K до трех. Проверив устойчивость системы критерием Рауса-Гурвица, увидим, что она стала устойчивой.
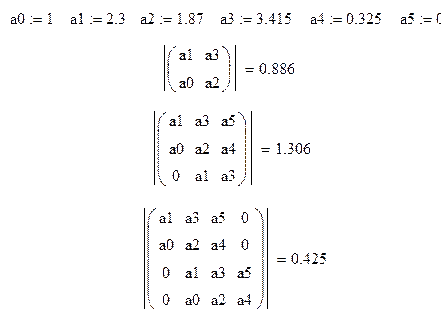
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.