Министерство образования РФ
ВлГУ
Кафедра КТРЭС
Выполнил:
студент гр. РЭ-100
Проверил:
1. Цель работы: проверить постулаты регрессионного анализа, построить математическую модель пассивного эксперимента, проверить адекватность получившейся модели и значимость коэффициентов регрессии.
2. Проверка постулатов регрессионного анализа
Постулаты регрессионного анализа сошлись.
3. Построение математической модели пассивного эксперимента
Математические модели строятся в виде полиномов.
Исходные данные:
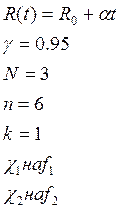
Определение математической модели производится с помощью метода наименьших квадратов.
Опытные данные:
|
R |
t1=170C |
t1=350C |
t1=500C |
|
R1 |
108 |
109 |
109.2 |
|
R2 |
107.9 |
109 |
109.2 |
|
R3 |
109.3 |
110.5 |
110.8 |
|
R4 |
108.9 |
110 |
110.2 |
|
R5 |
105.9 |
106.9 |
107.1 |
|
R6 |
106 |
107 |
107.3 |
|
|
107.7 |
108.7 |
109 |
На основании этих данных определяется математическая модель с помощью метода наименьших квадратов.
Данная математическая модель является линейным полиномом:
![]() - однофакторное пространство.
- однофакторное пространство.
|
|
|
|
|
|
|
|
|
|
|
Разность между точками модели и средними значениями между сечением:
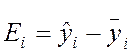 .
.
При МНК линия должна проводится таким образом, чтобы сумма квадратов отклонений между средними значениями и точками модели должна быть минимальной:
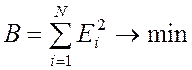
Для первого случая:
E1=0
E2=-0.2
E3=0.3
Для второго случая:
E1=0.18
E2=-0.19
E3=0.16
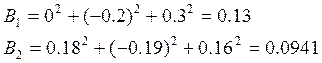
Сумма квадратов отклонений минимальна в случае В2.
|
t |
|
|
|
17 |
107.7 |
107.88 |
|
35 |
108.7 |
108.51 |
|
50 |
109 |
109.16 |
Условием нахождения минимума является выполнение следующих условий:
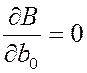 ,
, 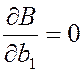 .
.
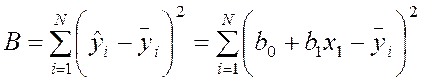 (2)
(2)
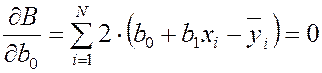 , тогда
, тогда
![]() .
.
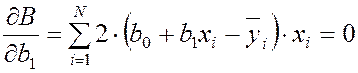 , тогда
, тогда
![]()
Получаем систему уравнений:
![]()
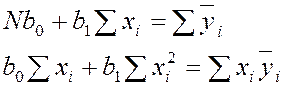 – система нормальных
уравнений.
– система нормальных
уравнений.
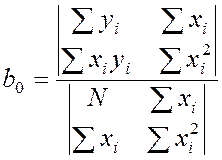 ;
;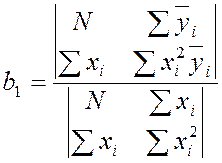 ;
;
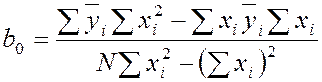 ;
;
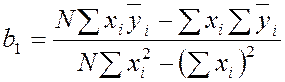 .
.
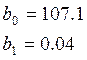
Математическая модель:
![]()
4. Проверка адекватности модели.
Проверка адекватности производится при помощи критерия Фишера:
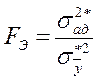 , где :
, где :
![]() –
дисперсия адекватности;
–
дисперсия адекватности;
![]() –
дисперсия воспроизводимости.
–
дисперсия воспроизводимости.
Если FЭ <FТ при заданном р, то считается, что модель адекватна, в противном случае – неадекватна.
![]() ,
,
![]() .
.
С использованием этого находится ![]() :
:
![]() , где k +1 определяет число
коэффициентов регрессии, k определяет число факторов.
, где k +1 определяет число
коэффициентов регрессии, k определяет число факторов.
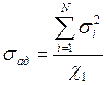 , где
, где ![]() .
.
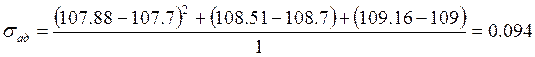
Дисперсия воспроизводимости – это дисперсия среднего значения выходного параметра.
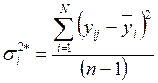 , где n
– число параллельных опытов.
, где n
– число параллельных опытов.
Дисперсия в сечении:
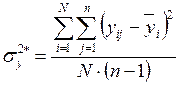 –
дисперсия выходного параметра y.
–
дисперсия выходного параметра y.
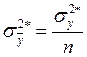 –
дисперсия среднего значения выходного параметра.
–
дисперсия среднего значения выходного параметра.
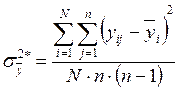 .
.
![]()
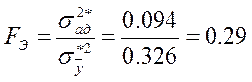
5. Проверка значимости коэффициентов регрессии
Значимость
коэффициентов регрессии проверяется в сопоставлении с ошибками эксперимента.
Считается, что коэффициент значим, если его абсолютная величина ![]() , где
, где ![]() –
ошибка при его определении.
–
ошибка при его определении.
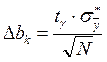 ,
,
![]() .
.
В данном случае при g=0.95, tg=2.02, ![]() ,
,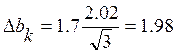
R0: 107,1 > 1,98 – коэффициент значим
a: 0,04 < 1,98 – коэффициент значим
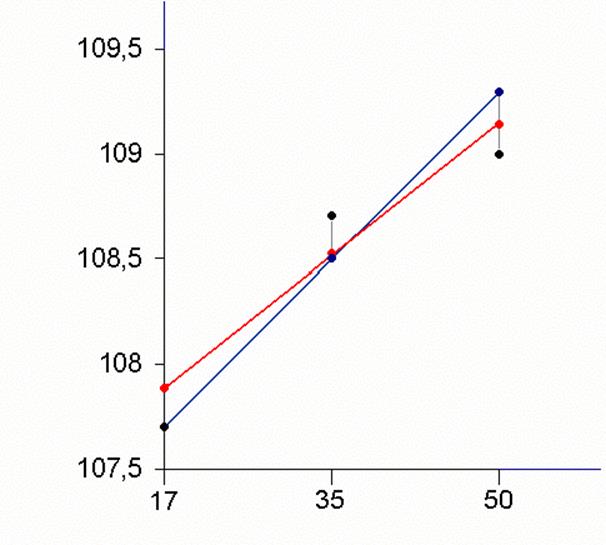
Графическая интерпретация полученных данных приведена на рисунке 1.
Рис. 1. График зависимости R от DT.
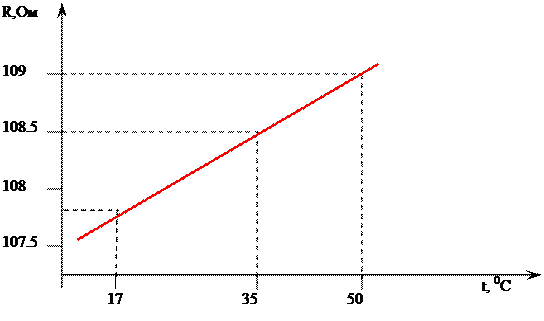 |
Рисунок 1
6. Вывод: в процессе выполнения лабораторной работы было произведено ознакомление с методами обработки результатов пассивного эксперимента, построения математических моделей, проверки адекватности модели. Была построена и проверена на адекватность математическая модель зависимости сопротивления резистора от температуры.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.