Проведение и обработка результатов пассивного эксперимента

Федеральное агентство по образованию

Владимирский государственный университет

Факультет радиофизики электроники и медицинской техники

Кафедра конструирование и технологии радиоэлектронных средств

Лабораторная работа № 4

Проведение и обработка результатов пассивного эксперимента.

Выполнила:

студентка гр. Р-105

Проверил:

Владимир  2007

Цель работы: Построение математической модели процесса изменения сопротивления резисторов от температуры.

Тип элемента и его номинальное значение.

В качестве однотипных радиоэлементов использовались резисторы с номинальным сопротивлением 1 кОм, в качестве измерительного прибора использовался мультиметр.

Выполнение работы:

В таблице 1 представлены значения сопротивлений резисторов при температуре 20, 40, 60^оС.

Сопротивления, Ом	Т1 = 20	Т2 = 40	Т3 = 60
R7	111,5	111,5	111,7
R8	110,3	109,8	109,4
R9	110,3	110,2	110,1
R10	111,2	110,9	110,9
R11	108,6	110,8	108
R12	114,0	113,4	113,1
Rср	110,98	111,10	110,53

На рис.1 изображены точки, соответствующие данным значениям сопротивлений, построена зависимость у = b₀ + b₁x (синяя линия).

Рис. 1 Значения сопротивлений резисторов при различной температуре показаны точками, красными точками отмечены средние значения сопротивлений в каждом интервале температур, синей линей представлена зависимость у = b₀ + b₁x.

В данной работе проверяется адекватность линейной модели у = b₀ + b₁x. Для данного случая: R = b₀ + b₁T. Коэффициенты b₀ и b₁ , определяемые по методу наименьших квадратов, находятся по формулам:

; .

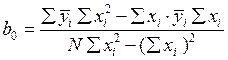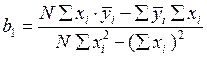Для данного случая:

; .

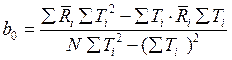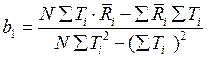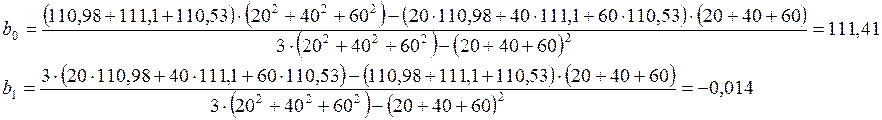Теперь строится зависимость R = 111,41 -0,014 ΔT (рис.1 – синяя линия). Т = 20, 40, 60 ^оС

Значения R для данных температур приведены в таблице 2.

Проверка адекватности модели производится при помощи критерия Фишера:

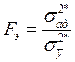, где  - дисперсия адекватности,  - дисперсия воспроизводимости.

Экспериментальное значение необходимо сравнить с табличным . Число степеней свободы  определяются:,        .

.

N – число опытов, k – число факторов ,т.е. равно числу коэффициентов регрессии.

При уровне значимости р = 0,05 и чисел степеней свободы  и  критерий Фишера равен: .

Дисперсия адекватности равна:      .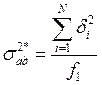

где  .

 Ом.

Значения  представлены в таблице 2.

Тогда дисперсия адекватности равна:

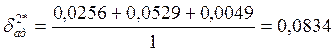
Дисперсия воспроизводимости - это дисперсия среднего значения выходного параметра . Дисперсия в i-ом сечении находится:

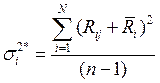, где n – число параллельных опытов.

Дисперсия выходного параметра определяется:

.

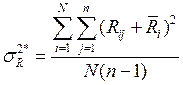Тогда дисперсия воспроизводимости будет определяться:

.

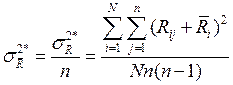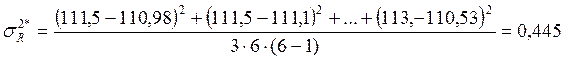Ом².

Таким образом, экспериментальный критерий Фишера равен:

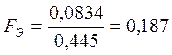
Поскольку , то можно считать, что модель адекватна.

Таблица 2  Рассчитанные значения , и .

Проверка значимости коэффициентов регрессии.

Значимость коэффициентов регрессии проверяется в сопоставлении их абсолютной величины с ошибками эксперимента. Ошибка определяется по формуле:

.

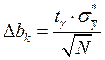Квантиль  находится в зависимости от числа степеней свободы  и доверительной вероятности γ = 0.95, .

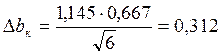
Поскольку ошибка не превышает ни один из коэффициентов регрессии (b₀ = 111,41, b₁=-0,014), то можно считать, что коэффициент b₁ является не значимым.

Выводы: В ходе лабораторной работы определены значения сопротивлений резисторов при различных значениях  температуры. С помощью метода наименьших квадратов подобрана линейная модель.

Поскольку полученное экспериментальное значение критерия Фишера не превышает табличного значения (для данных степеней свободы и данного уровня значимости), выбранную модель можно считать адекватной.

Ошибка при определении коэффициента регрессии b₁ превышает абсолютное значение коэффициента, следовательно, данный коэффициент является не значимым.