Анализ прохождения электрических колебаний через линейные цепи электронных устройств, страница 3

Отношение комплексных амплитуд выходного и входного гармонических напряжений одной и той же частоты определяет частотный коэффициент передачи (чаще просто коэффициент или функцию передачи)линейного четырехполюсника:

где w — круговая частота входного сигнала.

В линейных цепях  не зависит от амплитуды колебаний, но может меняться с частотой ω. Модуль коэффициента передачи К(w)=|К(w)| называют амплитудночастотной характеристикой (АЧХ), а аргумент j(w) — фазочастотной характеристикой (ФЧХ) линейного четырехполюсника. В обычных усилителях АЧХ имеет один максимум, а ФЧХ изменяется монотонно в зависимости от частоты (рис. 3).

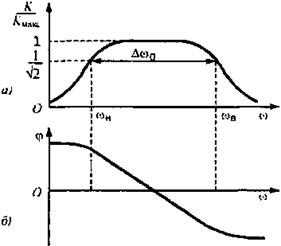
Рис. 3. Характеристики линейной цепи:

 а) — амплитудно-частотная; б) — фазочастотная

В общем виде получаем связь между спектрами входного  и выходного  колебаний.

Таким образом, для определения формы колебаний на выходе линейной цепи  при известном входном колебании надо реализовать следующий  порядок действий:

- рассчитать спектр входного колебания  с помощью прямого преобразования Фурье;

- комплексную амплитуду каждой гармонической составляющей спектра умножить на комплексную функцию передачи ;

- на последнем этапе из полученного спектра выходного колебания  с помощью обратного преобразования Фурье найти выражение для мгновенных значений выходного колебания .

В лабораторной работе прохождение сигналов через линейные цепи и каскадное включение четырехполюсников рассматривается на примере простейших дифференцирующей и интегрирующей цепей. Анализ этих цепей рассматриваемых раздельно проводится решением дифференциальных уравнений, а совместного включения – методом спектрального анализа.

В практике анализа цепей часто сложную цепь представляют в виде нескольких простых, для которых функции передачи определить легко или они уже известны. Типовым в этом случае будет представление одного сложного четырехполюсника в виде нескольких включенных последовательно, так что выход предыдущего соединяется со входом последующего. Такое соединение называется каскадным. Если четырехполюсник с функцией передачи K₁(jω) каскадно включен cо вторым четырехполюсником K₂(jω), то общая функция передачи со входа первого на выход второго будет равна

K(jω) = K₁(jω) K₂(jω).

2.2. Дифференцирующие цепи

Дифференцирующей цепью называется линейный четырехполюсник, в виде последовательной RС-цепи, на входе которой действует напряжение u_вх(t), а выходное напряжение u_вых(t) снимается с резистора R(рис. 4, а). RС-цепь может осуществлять линейную операцию дифференцирования входного сигнала.

                     

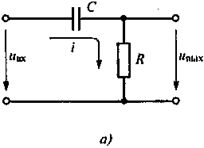
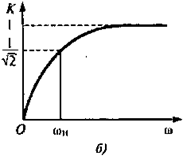
Рис. 4. Дифференцирующая цепь:

а — схема; б — АЧХ

Чтобы определить частотный коэффициент передачи дифференцирующей цепи, запишем комплексную амплитуду тока:

Выразив комплексную амплитуду выходного напряжения через ток U_вых = IR, находим частотный коэффициент передачи

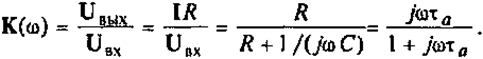
Здесь параметр t_a = RC — постоянная времени цепи.

Теперь, вычислив модуль частотного коэффициента передачи, определяем АЧХ дифференцирующей цепи

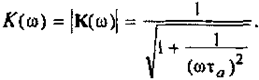
Из  графика АЧХ (рис.4,б) следует, что полоса пропускания дифференцирующей цепи ограничена только со стороны нижних частот.

Проанализируем прохождение импульсных сигналов через дифференцирующую цепь, подав на ее вход напряжение в виде прямоугольного видеоимпульса с амплитудой Е и длительностью t_и (рис. 5, а).

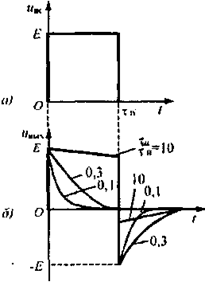
Рис. 5. Операция дифференцирования:

а — входной сигнал;  6— выходной сигнал