Цели работы:
1. исследование линейной цепи
2. проверка методами контурных токов и узловых потенциалов
Исходные данные:
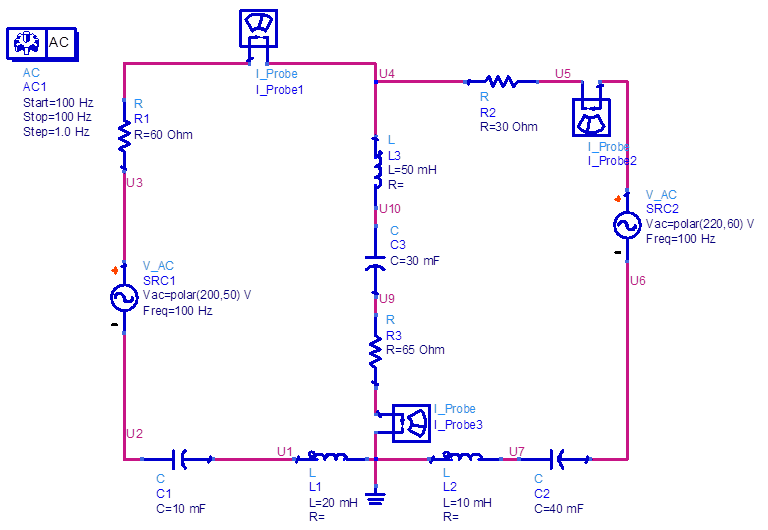
Дано:
f=100 Гц
R1=60 Ом
R2=30 Ом
R3=65 Ом
E1=200![]() 50°
50°
E2=220![]() 60°
60°
C1=10 мФ
C2=40 мФ
C3=30 мФ
L1=20 мГн
L2=10 мГн
L3=50 мГн
1. Определение комплексных токов ветвей методом контурных токов:
![]() =200
=200![]() 50°=(128+j153)B
50°=(128+j153)B
![]() =220
=220![]() 60°=(110+j190,5)B
60°=(110+j190,5)B
Комплексное сопротивление ветвей:
ω=2πf=2*3,14*100=628 рад/с
XL1= ωL1 =628*20*10-3=12,56 Ом
XC1=1/ωC1=1/628*10*10-3=0,16 Ом
Z1=R1+j(XL1- XC1)=60+j(12,56-0,16)=60+j12,4=61,2![]() 11,6°
Ом
11,6°
Ом
XL2= ωL2 =628*10*10-3=6,28 Ом
XC2=1/ ωC2=1/628*40*10-3=0,04 Ом
Z2=R2+j (XL2-XC2 )=30+j6,24=30,6![]() 11,7° Ом
11,7° Ом
XL3= ωL3 =628*50*10-3=31,4 Ом
XC3=1/ ωC3=1/628*30*10-3=0,05 Ом
Z3=R3+j (XL3-XC3)=65+j31,35=67,7![]() 25,7° Ом
25,7° Ом
Составим систему уравнений для контурных токов:
![]() Z11
Z11![]() l+Z12
l+Z12![]() ll=
ll=![]() 1
1
Z21![]() l+Z22
l+Z22![]() ll=
ll=![]() 2,
2,
Где
Z11=Z1+Z3=60+j12,4+65+j31,35=125+j43,75=132,4![]() 19,3° Ом
19,3° Ом
Z12=Z21=Z3=65+j31,35=67,7![]() 25,7° Ом
25,7° Ом
Z22=Z2+Z3=30+j6,24+65+j31,35=95+j37,59=102,1![]() 21,6° Ом
21,6° Ом
Решим систему уравнений с помощью определителей:
![]() ;
;
![]()
Где ![]() Z=
Z=![]() =132,4
=132,4![]() 19,3°*102,1
19,3°*102,1![]() 21,6°-(67,7
21,6°-(67,7![]() 25,7°)2=13518,04
25,7°)2=13518,04![]() 40,9°-4583,29
40,9°-4583,29![]() 51,4° = =10217,6+j8850,8-2859,4-j3581,9=7358,2+j5268,9=9050,1
51,4° = =10217,6+j8850,8-2859,4-j3581,9=7358,2+j5268,9=9050,1![]() 35,6°
35,6°
Где ![]() 1=
1=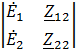 =200
=200![]() 50°*102,1
50°*102,1![]() 21,6°- 220
21,6°- 220![]() 60°*67,7
60°*67,7![]() 25,7°=20420
25,7°=20420![]() 71,6°-14894
71,6°-14894![]() 85,7° = =6445,5+j19376-1116,7-j14852=5328,8+j4524=6990,2
85,7° = =6445,5+j19376-1116,7-j14852=5328,8+j4524=6990,2![]() 40,3° В·Ом
40,3° В·Ом
Где ![]() 2=
2=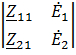 =132,4
=132,4![]() 19,3°*220
19,3°*220![]() 60°-67,7
60°-67,7![]() 25,7°*200
25,7°*200![]() 50°=29128
50°=29128![]() 79,3°-13540
79,3°-13540![]() 75,7° = =5408+j28621-3344,3-j13120,4=2063,7+j15500,6=15637,3
75,7° = =5408+j28621-3344,3-j13120,4=2063,7+j15500,6=15637,3![]() 82,4° В·Ом
82,4° В·Ом
![]() =6990,2
=6990,2![]() 40,3° / 9050,1
40,3° / 9050,1![]() 35,6°=0,772
35,6°=0,772![]() 4,7°=(0,769+j0,063)A
4,7°=(0,769+j0,063)A
![]() =15637,3
=15637,3![]() 82,4° / 9050,1
82,4° / 9050,1![]() 35,6°=1,727
35,6°=1,727![]() 46,8°=(1,182+j1,258)A
46,8°=(1,182+j1,258)A
Токиветвей:
![]() =0,772
=0,772![]() 4,7°A
4,7°A
![]() =1,727
=1,727![]() 46,8°A
46,8°A
![]() +
+ ![]() ll =0,772
ll =0,772![]() 4,7°+1,727
4,7°+1,727![]() 46,8°=0,769+j0,063+1,182+j1,258 =1,951+j1,321=2,356
46,8°=0,769+j0,063+1,182+j1,258 =1,951+j1,321=2,356![]() 34,1°A
34,1°A
2. Определение комплексных чисел токов ветвей методом узлов. потенциалов.
Узловое напряжение схемы:
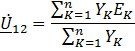
Где ![]() ;
;
![]() ;
;![]()
Y1=1/61,2![]() 11,6° = 0,016
11,6° = 0,016![]() -11,6°=(0,015-j0,003) См
-11,6°=(0,015-j0,003) См
Y2=1/30,6![]() 11,7° = 0,032
11,7° = 0,032![]() -11,7°=(0,031-j0,006) См
-11,7°=(0,031-j0,006) См
Y3=1/67,7![]() 25,7° =0,014
25,7° =0,014![]() -25,7°=(0,012-j0,006) См
-25,7°=(0,012-j0,006) См
U12 =0,016![]() -11,6°*200
-11,6°*200![]() 50°+0,032
50°+0,032![]() -11,7°*220
-11,7°*220![]() 60°/0,015-j0,003+0,031-j0,006+0,012-j0,006 =3,2
60°/0,015-j0,003+0,031-j0,006+0,012-j0,006 =3,2![]() 38,4° +
7,04
38,4° +
7,04![]() 48,3°/0,058-j0,015=2,51-j1,98+4,68+j5,25/0,058-j0,015=
=7,19+j7,23/0,058-j0,015=10,2
48,3°/0,058-j0,015=2,51-j1,98+4,68+j5,25/0,058-j0,015=
=7,19+j7,23/0,058-j0,015=10,2![]() 45,1°/0,059
45,1°/0,059![]() -14,5°=172,8
-14,5°=172,8![]() 59,6°=(87,44+j149,04) В
59,6°=(87,44+j149,04) В
Комплексные токи ветвей:
I1=128+j153-87,44- j149,04/61,2![]() 11,6° =40,56
+j3,96/61,2
11,6° =40,56
+j3,96/61,2![]() 11,6° = 40,75
11,6° = 40,75![]() 5,57°/61,2
5,57°/61,2![]() 11,6°= =0,665
11,6°= =0,665![]() -6,03° A
-6,03° A
I2=110+j190,5-87,44- j149,04/30,6![]() 11,7° =22,56+j41,46/30,6
11,7° =22,56+j41,46/30,6![]() 11,7° = 47,2
11,7° = 47,2![]() 61,44°/30,6
61,44°/30,6![]() 11,7° = =1,542
11,7° = =1,542![]() 49,74° A
49,74° A
I3 =172,8![]() 59,6° /
59,6° / ![]() 67,7
67,7![]() 25,7° =2,552
25,7° =2,552![]() 33,9° A
33,9° A
Вывод:
В выполнении данной лабораторной работы было произведено:
1) определение комплексных токов ветвей методом контурных токов и получены следующие результаты:
![]() =0,772
=0,772![]() 4,7°A
4,7°A
![]() =1,727
=1,727![]() 46,8°A
46,8°A
![]() +
+ ![]() ll =2,356
ll =2,356![]() 34,1°A
34,1°A
2) определение комплексных чисел токов ветвей методом узловых потенциалов и также получены следующие значения:
I1=0,665![]() -6,03° A
-6,03° A
I2 =1,542![]() 49,74° A
49,74° A
I3 =2,552![]() 33,9° A
33,9° A
Результаты олученные при использовании первого метода немного отличаются от результатов по второму методу, что можно списать на погрешность расчётов.
3) По полученым расчётным результатам была построена векторная диаграмма токов.
4)Было произведено исследование цепи с помощью САПР ADS. Сравнив полученные результаты, можно заключить, что токи в цепи посчитаны правильно, поскольку их значения практически совпадают.
5)В целом выполнение этой лабораторной работы помогло освоить важнейшие методы определения токов в линейной цепи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.