Мощный транзистор НЧ. Методы и схемы для измерения параметров транзистора, страница 3

2. 2. Граничная частота коэффициента передачи тока в схеме с ОБ.

Граничная частота коэффициента передачи тока f_α – та частота, на которой значение α  снижается на 3 дБ от своего значения на низкой частоте. Т.к. на низкой частоте значение α ≈ 1, то f_α определяется как частота, на которой α = 0,7. В схеме с ОЭ граничная частота всегда ниже его граничной частоты в схеме с ОБ.

Определить граничную частоту можно также с помощью схемы, изображенной на Рис. 2. Для этого потенциометром жестко устанавливается положение, при котором

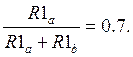
Затем, изменяя частоту на генераторе, добиваются нулевых показаний милливольтметра, что говорит о том, что текущая частота является граничной частотой коэффициента передачи тока.

Для более точной установки значения α = 0,7 лучше использовать два резистора номиналами, например, R1 = 280 Ом, а R2 = 120 Ом. Тогда схема для измерения граничной частоты коэффициента передачи тока транзистора, включенного по схеме с общей базой, будет выглядеть так:

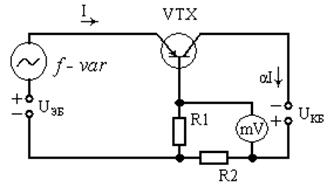
Рис. 3. Схема для измерения граничной частоты коэффициента передачи тока f_α

Для измерений выберем транзистор ГТ703А. U_КБ = 2 В, U_ЭБ = 2 В; R1 = 280 Ом, R2 = 120 Ом, номинальные значения сопротивлений соответствуют ряду Е192 (допуск ±5%); сигнал с генератора 10 мВ.

Структура погрешности.

Погрешность измерений в данном случае складывается из:

1. Погрешность установки сопротивлениями R1 и R2 соотношения 0.7: погрешность R1 (допуск) – инструментальная, систематическая, аддитивная (DR1 = 0.005∙R1), погрешность R2 (допуск) – инструментальная, систематическая, аддитивная (DR2 = 0.005∙R2).

2. Чувствительности вольтметра – погрешность цены деления – случайная, аддитивная, методическая (s_в = 0.05 мВ).

3. Погрешности установки частоты – инструментальная, случайная, мультипликативная ().

Для подсчета общей случайной погрешности найдем коэффициент для пересчета погрешности вольтметра в погрешность определения граничной частоты.

Модуль коэффициента передачи тока эмитера зависит от частоты следующим образом:

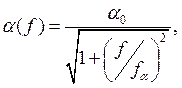
где – значение коэффициента передачи тока эмиттера на низкой частоте,  – угловая граничная частота. Вид этой зависимости представлен на Рис. 4:

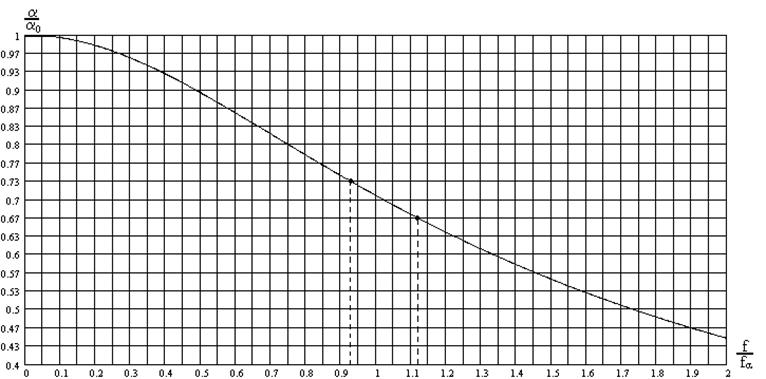
Рис. 4. Зависимость модуля коэффициента передачи тока эмиттера от частоты

Участок, на котором a[0.67;0.73], можно считать линейным. Найдем весовой коэффициент, связывающий погрешность измерения a с погрешностью измерения граничной частоты:

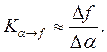
Из зависимости видно, что 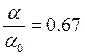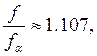при  а при 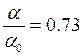 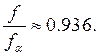Можно вычислить весовой коэффициент:

Как было показано ранее, погрешность вольтметра приводит к погрешности определения коэффициента передачи тока:

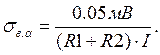
Погрешность, связанную с чувствительностью вольтметра, можно пересчитать в погрешность определения  с помощью весового коэффициента 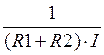. (R1+R2) = 400 Ом, пусть I = 1 мА, тогда  Тогда погрешность определения коэффициента передачи тока приведет к погрешности определения частоты:

Общая случайная погрешность измерений:

Для подсчета общей систематической погрешности найдем коэффициент для пересчета погрешности сопротивлений в погрешность определения граничной частоты.

Коэффициент передачи тока определяется соотношением:

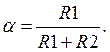
Систематическая погрешность в этом случае:

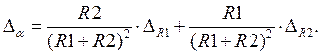
Зная, что R1 = 280 Ом, R2 = 120 Ом, DR1 = 0.005∙R1, DR2 = 0.005∙R2, найдем Da:

0.0021

Погрешность определения коэффициента передачи тока приведет к погрешности определения частоты:

Общая систематическая погрешность измерений:

Выполняется условие  тогда  Таким образом,  погрешность измерения граничной частоты коэффициента передачи тока транзистора, включенного по схеме с общей базой, составляет 0.6%.

2. 3. Входное сопротивление транзистора, включенного по схеме с ОБ.

Входное сопротивление (на частоте 1 кГц) транзистора можно измерить по схеме (Рис. 5.).

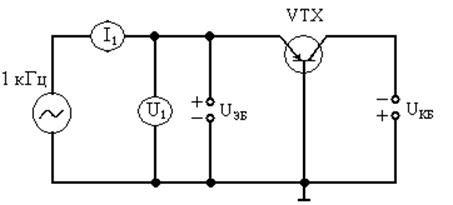
Рис. 5. Схема для измерения входного сопротивления транзистора.

На входные зажимы транзистора подается сигнал частотой 1 кГц с генератора низкой частоты. С помощью вольтметра и амперметра измеряются соответственно напряжение U₁ и ток I₁, входное сопротивление находится по формуле: