Анализ устойчивости системы, используя метод Рауса - Гурвица

Задание.

По известным нулям и полюсам:

1. Записать передаточную функцию системы.
2. Изобразить структурную схему системы.
3. Записать дифференциальное уравнение системы.
4. Найти и построить АЧХ, ФЧХ, ЛАЧХ, АФХ, переходную характеристику и весовую функцию.
5. Провести анализ устойчивости системы, используя метод Рауса - Гурвица.
6. Провести анализ устойчивости системы, используя метод Михайлова.
7. Провести анализ устойчивости системы, используя метод Найквиста.
8. Для не устойчивой системы дать рекомендации по обеспечению устойчивости.
9. Для устойчивой системы определить запасы устойчивости полученной системы.

Определим H(jw) и W(jw).

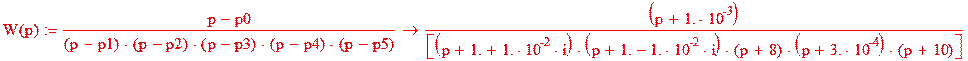
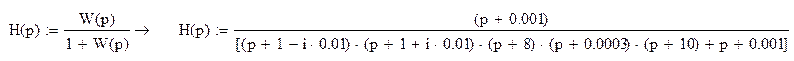
Структурная схема системы

Суть дифференциального уравнения заключается в том, что p заменяется на

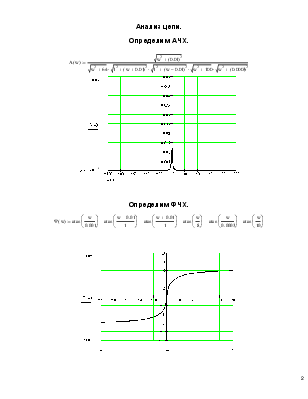
Анализ цепи.

Определим АЧХ.

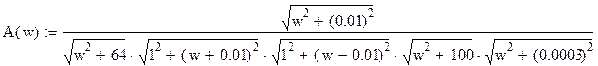
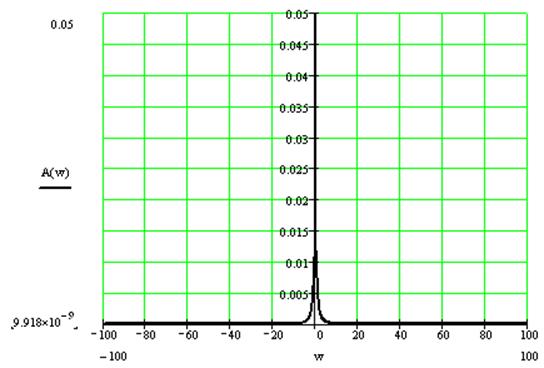
Определим ФЧХ.

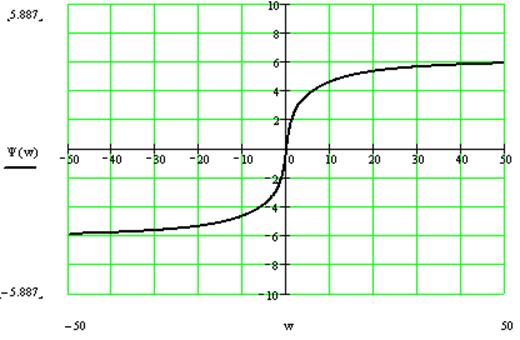
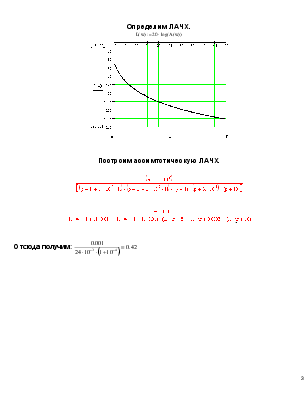
Определим ЛАЧХ.

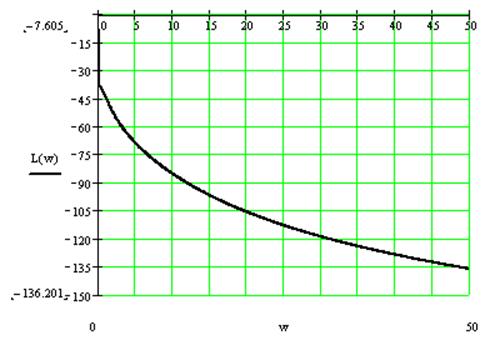
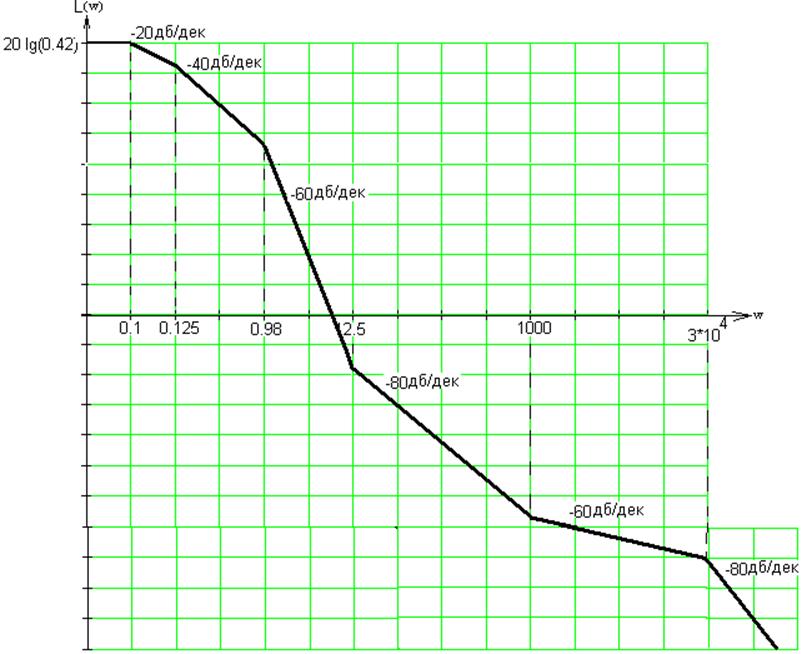
Построим ассимтотическую ЛАЧХ.

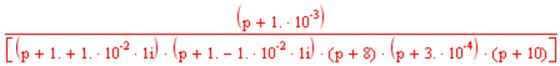
Отсюда получим: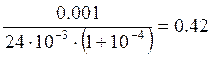

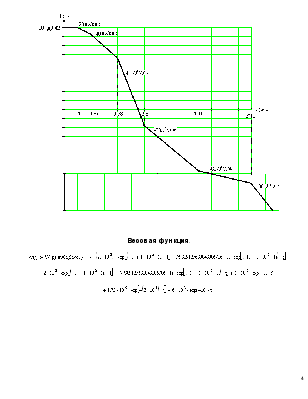
Весовая функция.

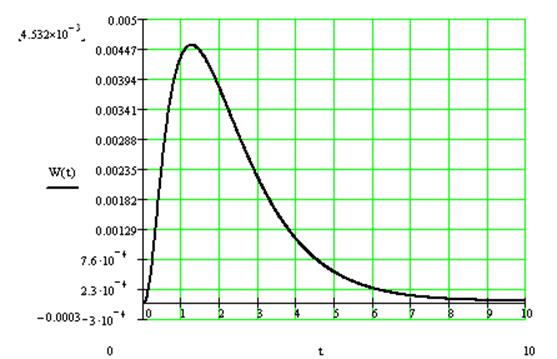
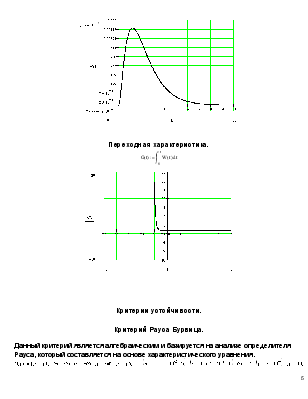
Переходная характеристика.

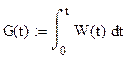
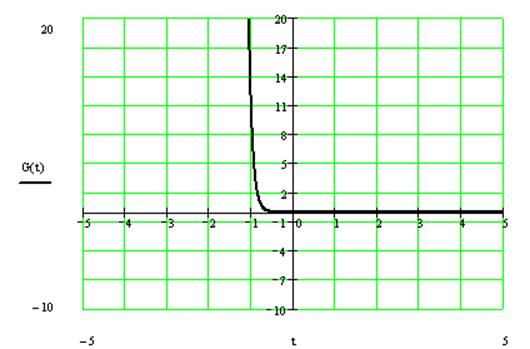
Критерии устойчивости.

Критерий Рауса Бурвица.

Данный критерий является алгебраическим и базируется на анализе определителя Рауса, который составляется на основе характеристического уравнения.

Необходимое условие выполнено: все члены характеристического уравнения не нулевые и не отрицательные. Проверим достаточное условие. Для этого составим матрицу определителя Рауса, составленную из коэффициентов характеристического уравнения замкнутой системы:

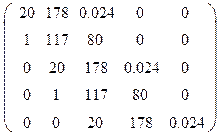
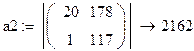
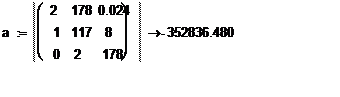
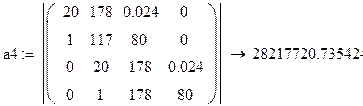
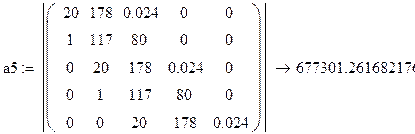
Видно, что третий определитель отрицателен, поэтому делаем вывод о том, что система не устойчива.

Критерий Михайлова.

Характеристический полином.

Необходимо, чтобы сумма аргументов корней равнялась .

Следовательно:

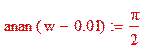
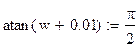
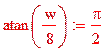
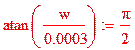
Необходимое условие выполнено.

Достаточное условие заключается в том, чтобы вектор кривой Михайлова при изменении частотыот 0 до  повернулся вокруг начала координат против часовой стрелки на угол .

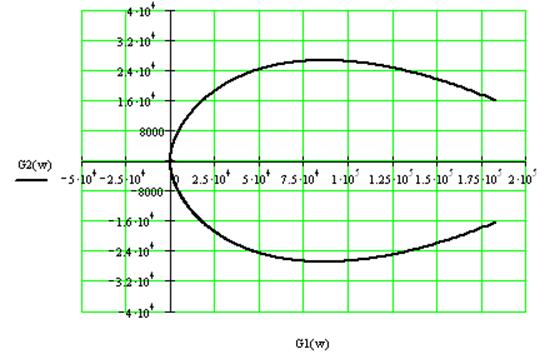
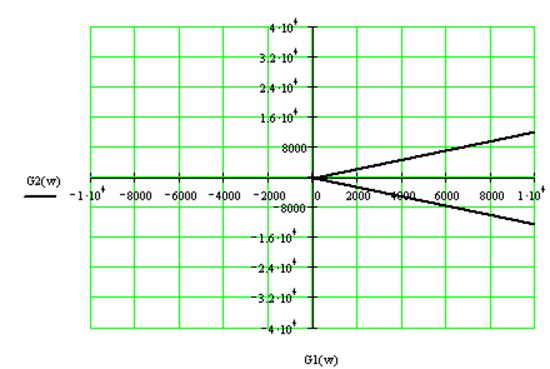
Видно , что вектор кривой Михайлова начинается в первой четверти и заканчивается в четвертой не заходит в другие. Т.е.система не устойчивая.

Критерий Найкреста.

Введем вспомогательную функцию.

Необходимо и достаточно, чтобы функция в плоскости комплексной переменной была замкнута и не охватывала точку (-1; j0)

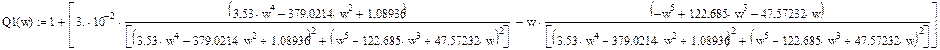
АФХ разомкнутой системы

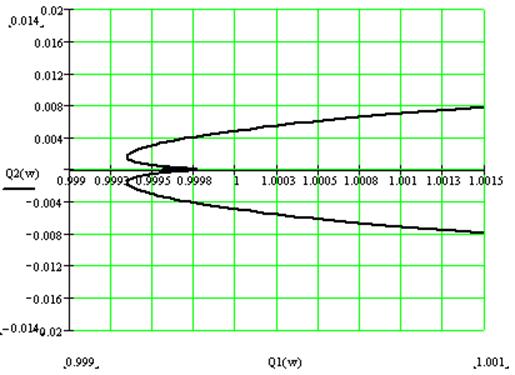
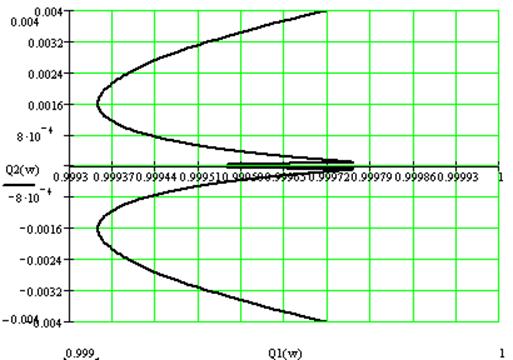
Так как функция терпит разрыв, то система не устойчива.

Рекомендации по устойчивости.

В данной системе можно предложить, изменить постоянные времени звеньев  или не нескольких звеньев.