Квазиоптимальные методы сложения разнесенных сигналов

Лекция 29. Квазиоптимальные методы сложения разнесенных сигналов              

Реализация оптимального объединения требует достаточно сложной аппаратуры, что не всегда компенсируется достигаемым выигрышем. Поэтому имеет смысл, рассмотреть квазиоптимальные методы, обеспечивающие помехоустойчивость близкую к оптимальной и, в то же время, проще реализуемые практически. Конкурентоспособность автовыбора и линейного сложения,  по сравнению с оптимальным, наряду с простотой реализации, так же базируется на том, что при их использовании не требуется учитывать уровень шумов в ветвях во всех случаях при линейном сложении и в случае близких уровней при автовыборе.

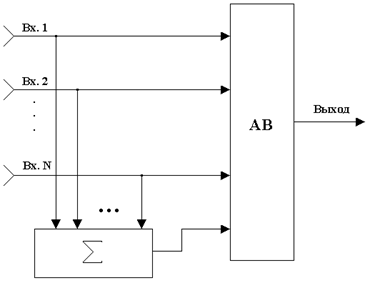
Объединение этих методов позволяет достигнуть, наряду с сохранением их преимуществ, эффективных результатов, близких к оптимальному сложению. Возможная структурная схема для этого случая приведена на рис.29.1, а диаграмма, описывающая свойства этой схемы, приведена на рис. 29.2.

Операция выбора сигнала максимального уровня (автовыбора - АВ) производится не из набора N входных разнесенных сигналов, а из расширенного набора, включающего кроме них еще один сигнал, предварительно полученный линейным сложением этих же N сигналов. Сигналы предполагаются предварительно сфазированными.

Рис. 29.1.                                                       Рис. 29.2.

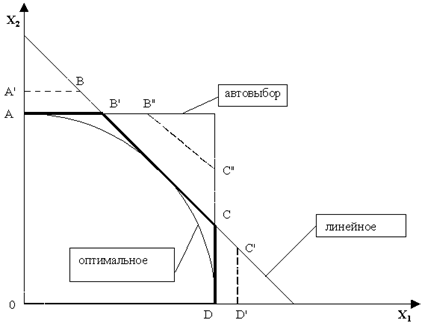
На диаграмме (рис. 29.2) для кратности разнесения N=2 иллюстрируется работа этой схемы. Здесь описывается зависимость между уровнями входных сигналов X₁ и Х₂, обеспечивающая постоянный уровень выходного сигнала. Диаграмма представляет собой ломаную линию АВСD. Эта линия касается окружности (оптимальное сложение) и представляет собой фрагмент многоугольника, в который вписана эта окружность.

Если коэффициент передачи подключаемого разнесенного сигнала в блоке автовыбора принять за единицу, то одинаковые весовые коэффициенты линейного сложения должны быть равны   1/√N. Любое отличие от этого значения приведет либо к преобладанию автовыбора (линия АВВ"С"СD), либо линейного сложения (линия А'В'ВСС'D'). В обоих случаях будет иметь место удаление от оптимального сложения и уменьшение помехоустойчивости.

Рис. 29.3.

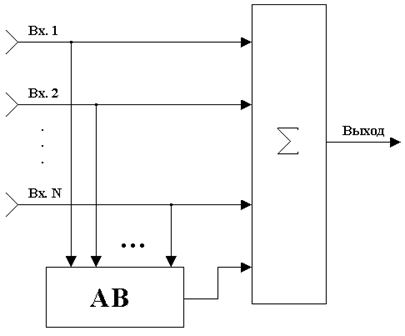Можно произвести сначала автовыбор, затем линейное сложение. Этому варианту соответствует схема и диаграмма, показанные на рис.29.3 и 29.4.

 Ребра многоугольника также касаются окружности (линия АВС), но в других точках. Наклон линий и места точек касания определяются соотношением коэффициентов передачи блоков автовыбора и линейного сложения (например образуя линию А'В'С'). Для случая N>2 многомерный многогранник также облегает гиперсферу, но имееет иной вид.

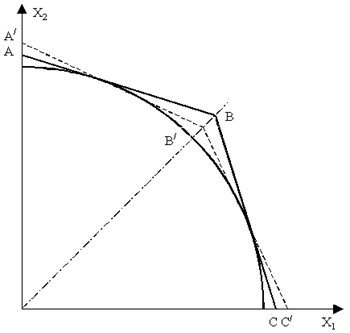Рис. 29.4.

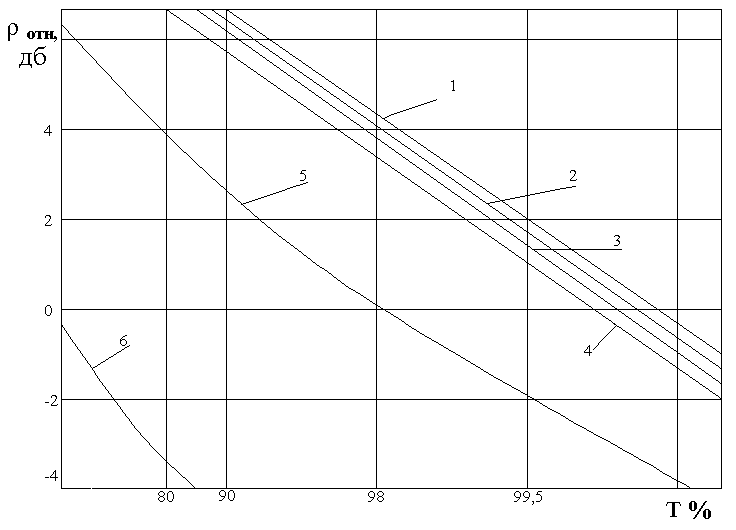
На рис.29.5 и рис.29.6 представлены графики, отражающие свойства рассмотренных схем квазиоптимального сложения. По оси ординат сложено нормированное отношение «сигнал/шум» ρ_отн относительно медианного уровня при приеме без разнесения, а по оси абсцисс - время, в течении которого превышается значение ρ_отн.

Кривые соответствуют следующим видам комбинирования сигналов: 1-оптимальное сложение; 2 – объединение согласно схеме на рис. 1.; 3 – объединение согласно схеме на рис. 2; 4 – линейное сложение; 5 – автовыбор; 6 – распределение  Рэлея  для приема без разнесения.

При этом считается, что при разнесенном приеме все сигналы флуктуируют независимо и имеют распределение Рэлея с одинаковыми параметрами.

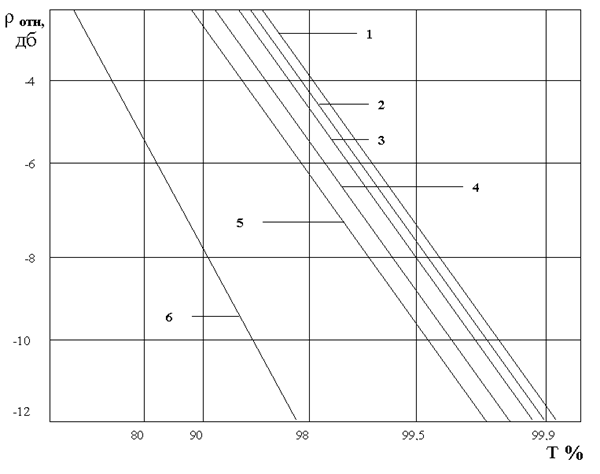Рис. 29.5.

Для схемы на рис.29.3 в диаграмме на рис.29.4 принимались такие же коэффициенты передачи блоков автовыбора и линейного сложения, как и для схемы на рис. 1, т.е. линия АВС описывается формулой             

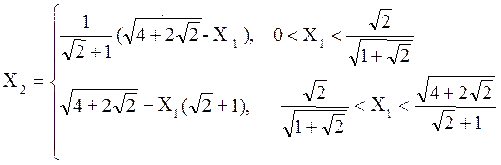
Обе схемы на рис.29.1 и  на рис.29.3 приближаются по помехоустойчивости к оптимальному сложению, однако схема на рис. 29.1 несколько более помехоустойчива.

Рис. 29.6.

Таким образом, квазиоптимальное объединение разнесенных сигналов может быть реализовано в виде комбинации автовыбора и линейного сложения. Реализация квазиоптимального сложения проще, чем оптимального, а характеристики помехоустойчивости приближаются к характеристикам при оптимальном сложении, что может служить рекомендацией к использованию квазиоптимальных схем объединения разнесенных сигналов.

Необходимость подстройки фаз складываемых сигналов может заметно усложнить метод обработки. Выбираемая точность подстройки фазы в блоках СП определит сложность их структуры. Если потребовать высокую точность подстройки, которая обеспечивается применением ФАП и обратных связей, то сложность может неоправданно возрасти.  Если же ограничиться ослабленными  требованиями, то при незначительном проигрыше структуру блоков сравнения и подстройки фазы можно значительно упростить, особенно с использованием дискретной подстройки фазы.

Фаза входного сигнала подстраивается под фазу опорного несколькими однотипными последовательными операциями, осуществляемыми в ячейках одинаковой структуры (на рис. 29.7. структура одной из ячеек номера  раскрыта).

В ней с опорным сигналом складывается входной сигнал этой ячейки в одном сумматоре – непосредственно, а в другом сумматоре  - после фазового сдвига на , где j – номер  этой ячейки в последовательном ряду, .

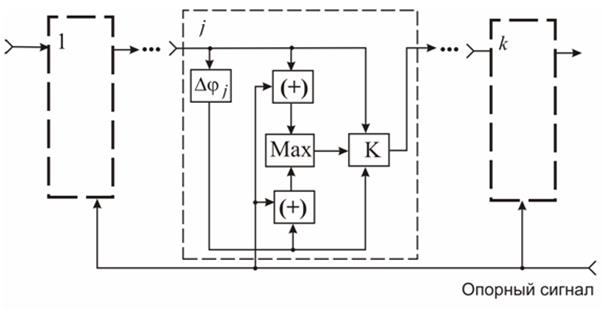Рис. 29.7.

Блок () сравнивает уровни получившихся сумм и с помощью коммутатора (К) на выход ячейки подключает тот из сигналов, которому соответствует большая по уровню сумма.  Этот сигнал более сфазирован с опорным, чем другой.

Таким образом, поскольку фазовые сдвиги в последовательно расположенных ячейках составляют 180; 90; 45 и т.д., то фазы выходных сигналов ячеек отличаются от фазы опорного сигнала соответственно не больше, чем на 90; 45; 22,5 и т.д. эта величина – максимально возможное различие. Считая, что относительный сдвиг фаз входного и опорного сигналов распределен равномерно в интервале , среднее уменьшение уровня сигнала из-за неточности фазирования при  прохождении  ячеек будет равно

.                               

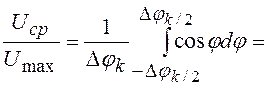
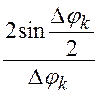
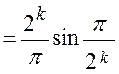Эта величина достаточно быстро стремится к единице, (при k=2 она равна 0,901; при k=3 она равна 0,975), поэтому практически требуется небольшое число ячеек.

Если для фазирования удовлетворительным считать 90%  - уровень (k=2), то структуру двух последовательных ячеек можно преобразовать в одну общую структуру с параллельной обработкой, как показано на рис. 8. В этой схеме из выходного сигнала получают еще три его копии, сдвинутые относительно него по фазе  соответственно на 90; 180и 270. Все они в сумматорах складываются с опорным сигналом.

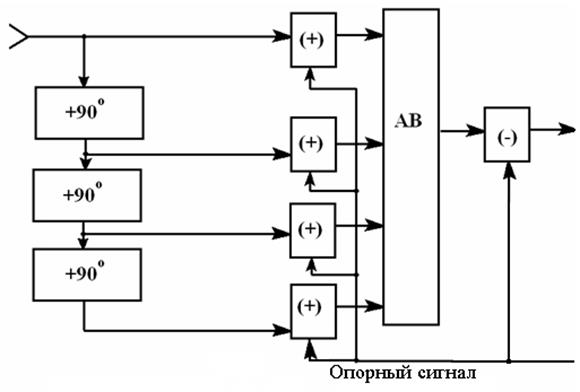Рис. 29.8

Далее из полученных четырех копий выбирается максимальная по уровню, с помощью блока автовыбора (АВ). Полученный сигнал будет наиболее сфазирован с опорным (с погрешностью не хуже 22,5). Если присутствие опорного сигнала в нем нежелательно, то он удаляется из выходного сигнала АВ в блоке вычитания (-).