Передаточные функции разомкнутой и замкнутой систем. Дифференциальное уравнение системы

1.  Задание.

По известным нулям и полюсам:

1. Записать передаточные функции разомкнутой и замкнутой систем.
2. Записать дифференциальное уравнение системы.
3. Нарисовать структурную схему системы.
4. Построить АЧХ, ФЧХ, ЛАЧХ, АФХ, переходную характеристику и весовую функцию.
5. Провести анализ устойчивости системы, используя метод Рауса - Гурвица.
6. Провести анализ устойчивости системы, используя метод Михайлова.
7. Провести анализ устойчивости системы, используя метод Найквиста.
8. Провести анализ устойчивости системы, используя ЛАЧХ системы.
9. Дать рекомендации по обеспечению устойчивости. Нарисовать структурную схему.
10. Определить запасы устойчивости полученной системы.

2.  Решение.

2.1.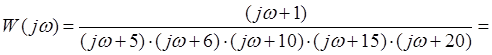     

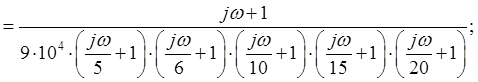
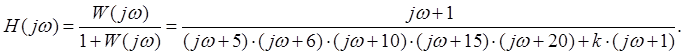
Т. о.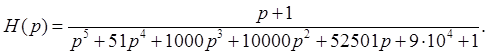

2.2.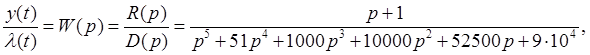       

тогда  Заменим

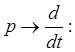
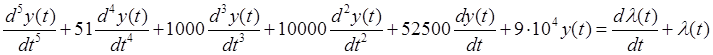
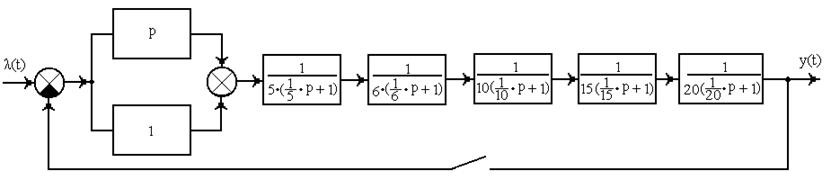
2.3. Возможная структурная схема системы:

2.4.      АЧХ: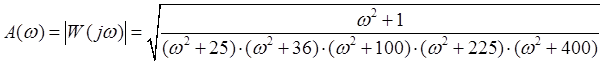

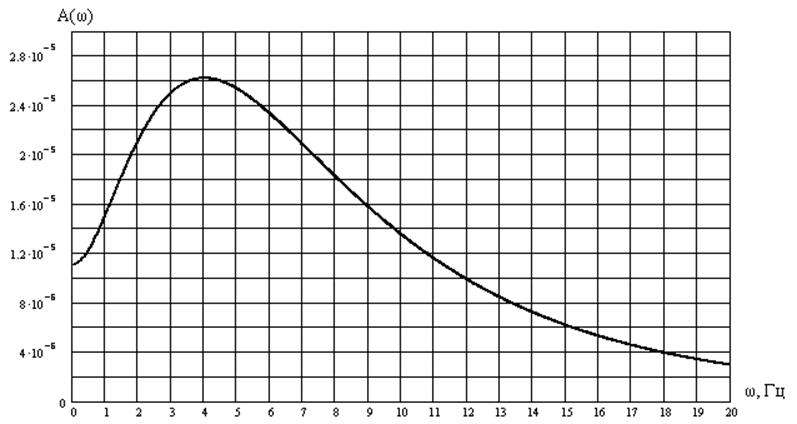
Рис. 1. АЧХ системы.

ФЧХ: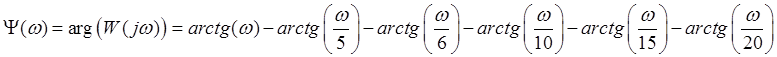

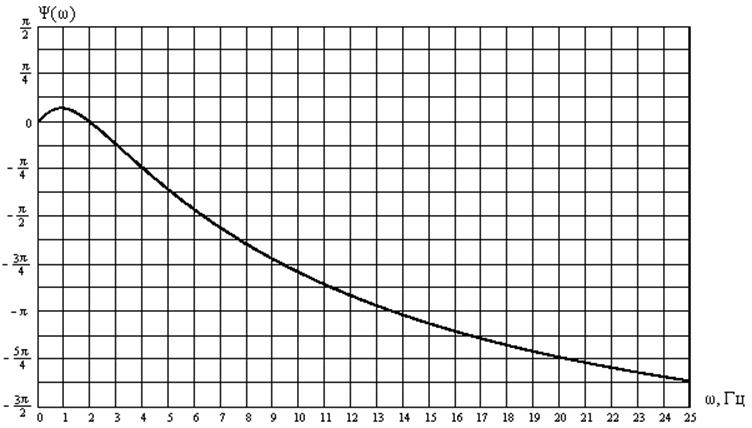
Рис. 2. ФЧХ системы.

ЛАЧХ: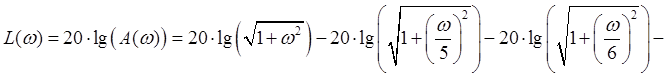

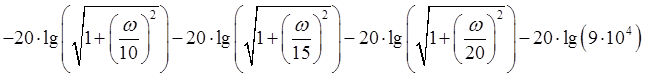
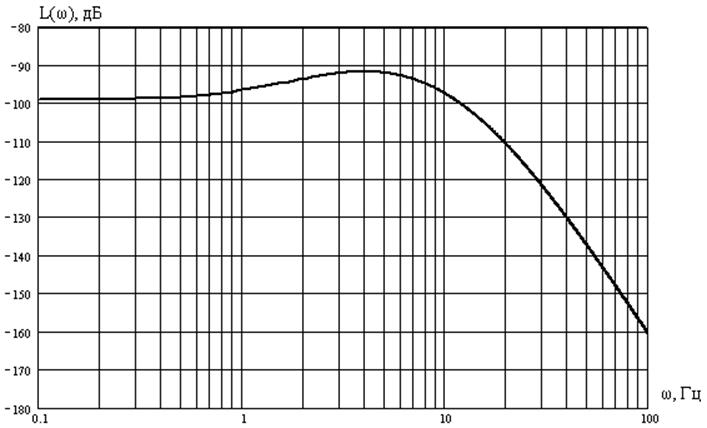
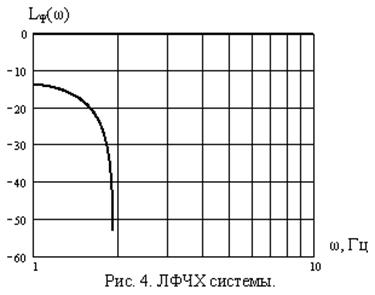Рис. 3. ЛАЧХ системы.

ЛФЧХ:

Асимптотическая ЛАЧХ строится по выражению для L(ω) (см. ранее), полагая что

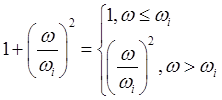
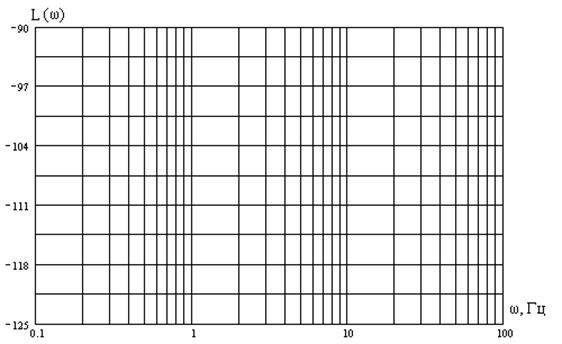
Рис. 5. Асимптотическая ЛАЧХ.

Весовая функция: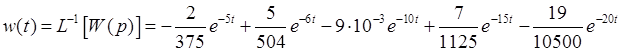

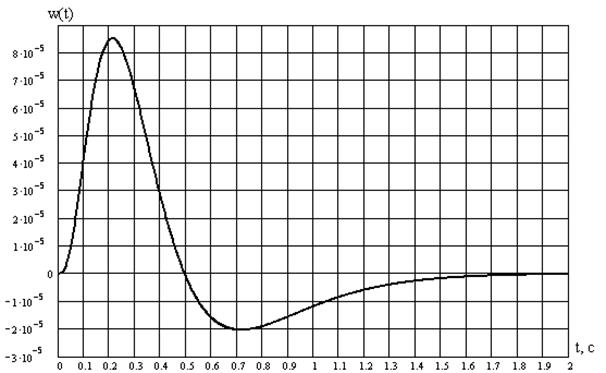
Рис. 6. Весовая функция.

Переходная функция:

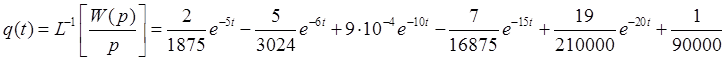
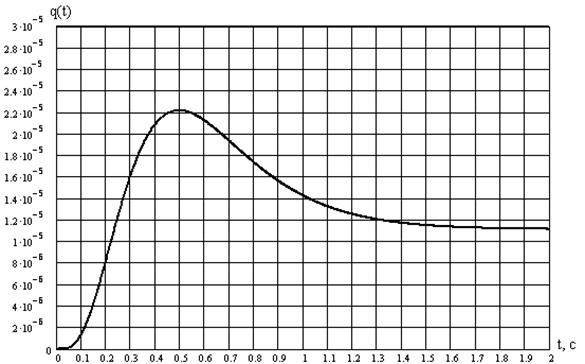
Рис. 7. Переходная характеристика.

2.5.      Анализ устойчивости системы по критерию Рауса - Гурвица заключается в вычислении определителей матриц, составленных из коэффициентов характеристического уравнения замкнутой системы:

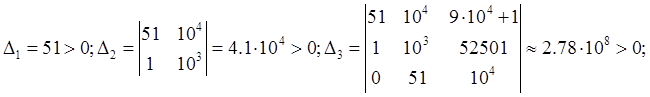
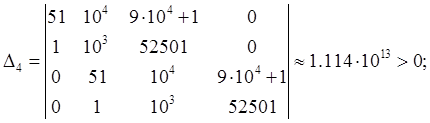
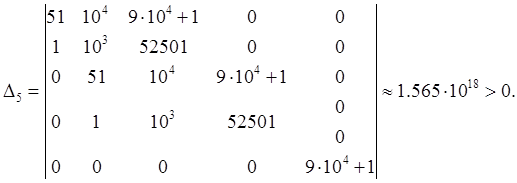
Т. к. все  и , то, согласно критерию Рауса - Гурвица, данная система является устойчивой.

2.6.      Анализ устойчивости системы по критерию Михайлова сводится к построению построению годографа Михайлова и анализу его поведения. Годограф Михайлова строится по точкам, задаваясь различными значениями ω (достаточно исследовать только одну ветвь годографа [ω изменяется от 0 до +∞]).

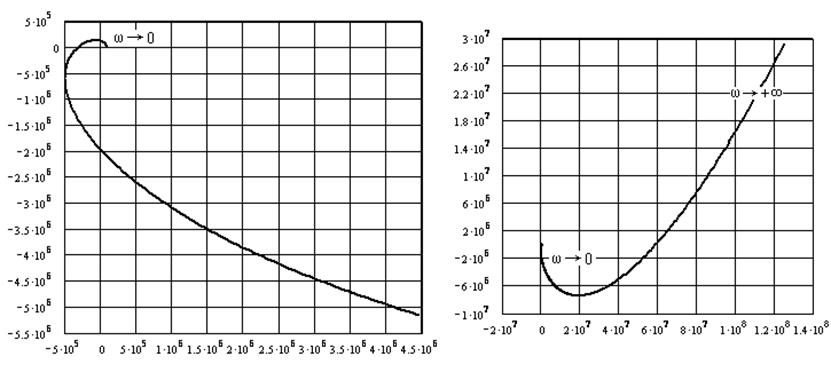
Рис. 8. К анализу устойчивости системы по критерию Михайлова.

Как видно годограф при изменении частоты от 0 до +∞ повернулся, не обращаясь в ноль, вокруг начала координат на угол . Т. о. согласно критерию Михайлова данная система является устойчивой.

2.8.      Критерий устойчивости Найквиста позволяет судить об устойчивости замкнутой системы по КЧХ разомкнутой системы. Если разомкнутая система устойчива, то для обеспечения её устойчивости в замкнутом состоянии необходима и достаточно, чтобы КЧХ разомкнутой системы не охватывала точку (-1; j0).

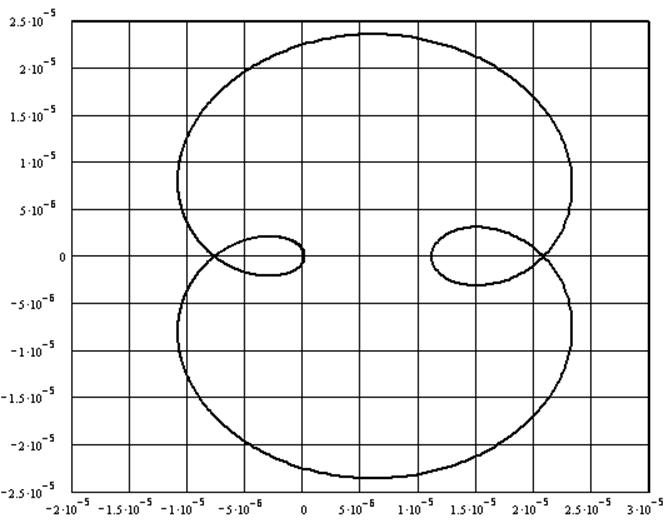
Рис. 9. АФХ разомкнутой системы.

АФХ разомкнутой системы не охватывает точку (-1; j0), поэтому по критерию Найквиста можно сказать, что данная система устойчива.

2.9.      Амплитудно-фазовый критерий устойчивости Найквиста применим и в случае изображения КЧХ в виде логарифмической амплитудной и фазовой частотных характеристик разомкнутой системы.

Так, если система устойчива в разомкнутом и замкнутом состояниях, то КЧХ разомкнутой системы не охватывает точку (-1; j0),  т. е. W(ω)<1 при Ψ(ω) = -π. Т. о. необходимым и достаточным условием устойчивости такой системы  является пересечение ЛАЧХ оси абсцисс раньше, ФЧХ пересечет линию, соответствующую ее фазовому сдвигу -π.

Т. к. ЛАЧХ разомкнутой системы не пересекает ось абсцисс, то по критерию Найквиста можно сказать, что данная система устойчива.

Запасы устойчивости по амплитуде и фазе не ограничены.