Задание
По заданному нулю и пяти полюсам передаточной функции записать выражение для передаточной функции разомкнутой и замкнутой систем. Найти дифференциальное уравнение системы. Нарисовать структурную схему. Найти и построить АЧХ, ФЧХ, АФХ разомкнутой системы. Проанализировать устойчивость работы системы методами Рауса-Гурвица, Михайлова, Найквиста. Построить графики ЛАЧХ, ЛФЧХ разомкнутой системы. Построить асимптотическую ЛАЧХ. Определить устойчивость работы системы по ЛАЧХ и ЛФЧХ. Если система устойчива, определить запасы устойчивости, в случае неустойчивости дать рекомендации по обеспечению устойчивости.
Исходные данные
k=250; р0=-0,2; р1=-0,2; р2= 0; р3=0; р4=-1+j0,8; р5=-1-j0,8;
1 Нахождение передаточной функции системы.
А) Выражение передаточной функции разомкнутой системы:
Находится числитель передаточной функции:
R(p)=(p-p0)k=250(p+0,2);
Находится знаменатель передаточной функции
G(p)=(p-p1)∙(p-p2)∙(p-p3)∙(p-p4)∙(p-p5)=
(p
+ 0,2)∙(p+1+j0,8)∙(p+1-j0,8)∙p2=![]() ;
;
Тогда выражение передаточной функции:
W(ω)=![]() =
=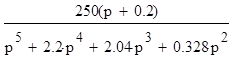 ;
;
Б) Выражение передаточной функции замкнутой системы:
Выражение передаточной функции замкнутой системы находится из формулы:
H(p)=![]() ;
;
В нашем случае:
H(p)=
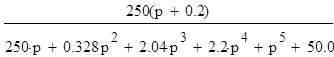 ;
;
2 Нахождение дифференциального уравнения системы.
А) Дифференциальное уравнение разомкнутой системы:
y(p)=H(p)*![]() ;
;
Подставив данные, получим:
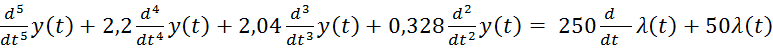 ;
;
Б) Дифференциальное уравнение замкнутой системы:
В дифференциальной форме передаточную функцию системы можно записать в следующем виде:
H(p)=![]()
Где ![]() реакция цепи на внешнее
воздействие;
реакция цепи на внешнее
воздействие;
![]() внешнее воздействие;
внешнее воздействие;
Тогда:
y(p)=H(p)*![]() ;
;
Подставив данные, получим:
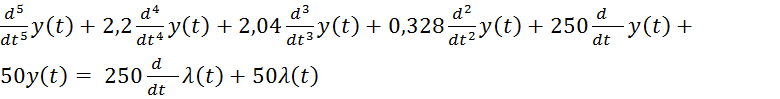 ;
;
3 Структурная схема цепи
Структурная схема цепи строится исходя из передаточной функции разомкнутой системы.
W(p)=
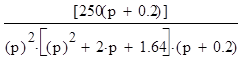 ;
;

Рисунок 1
Структурная схема цепи
4 АЧХ, ФЧХ, АФХ разомкнутой системы.
Для построения АЧХ необходимо найти модуль передаточной функции разомкнутой системы, заменив р на jω.
Передаточная функция примет вид:
W(jω)=
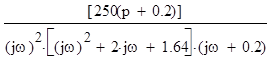 ;
;
Hайдем модуль функции:
W(jω)=
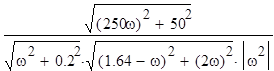 ;
;
Построим график:
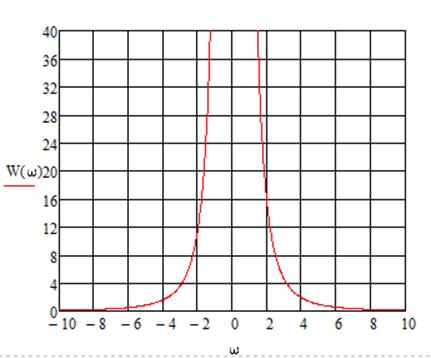
Рисунок 2
АЧХ разомкнутой системы
АЧХ разомкнутой системы.
ФЧХ системы – это аргумент передаточной функции:
![]() ;
;
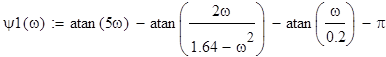 ;
;
![]() ;
;
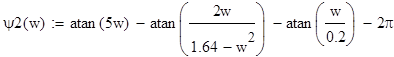 ;
;
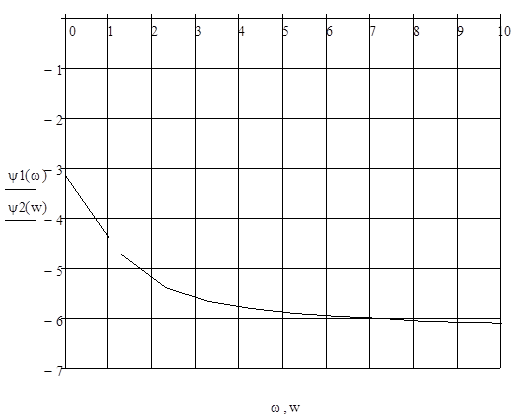
Рисунок 3
ФЧХ разомкнутой системы
Амплитудно-фазовая характеристика системы – зависимость мнимой составляющей передаточной функции от действительной составляющей.
Передаточная функция системы:
W(p)= 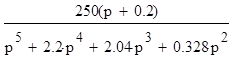 ;
;
В области частот:
W(jω)= 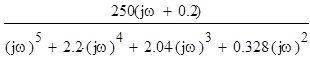 ;
;
Выделяем реальную и мнимую части:
W(jω)= 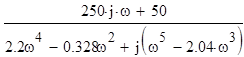 ;
;
Умножаем на комплексно-сопряженное выражение:
W(jω)= 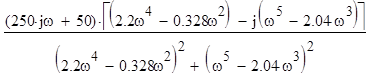 ;
;
В итоге получим:
W(jω)=
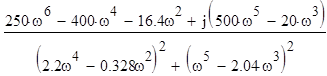 ;
;
Выделим действительную и мнимую части:
Действительная часть:
Re(W(ω))=
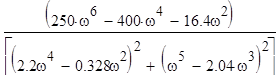 ;
;
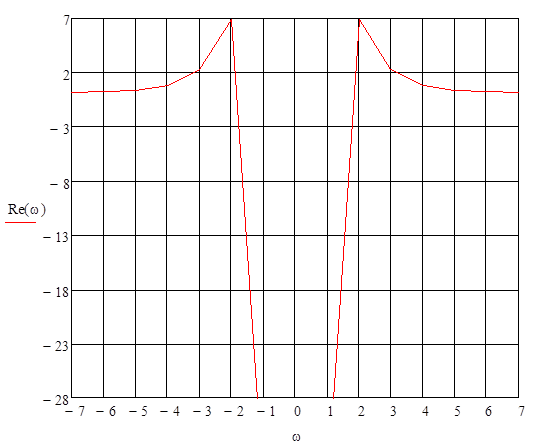
Рисунок 4
Действительная составляющая передаточной функции
Мнимая часть:
lm(W(![]() ))=
))=
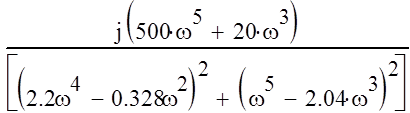 ;
;
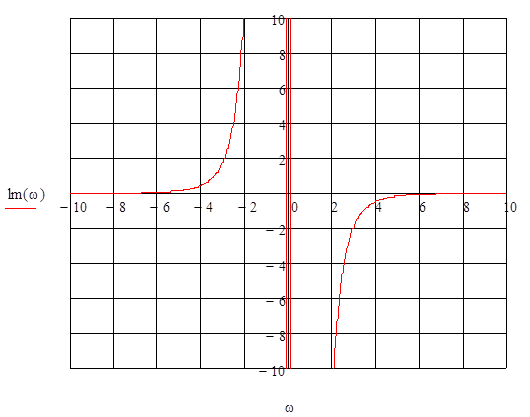
Рисунок 5
Мнимая составляющая передаточной функции
В декартовой системе координат по оси абсцисс принято откладывать действительную часть по оси абсцисс, а мнимую по оси ординат.
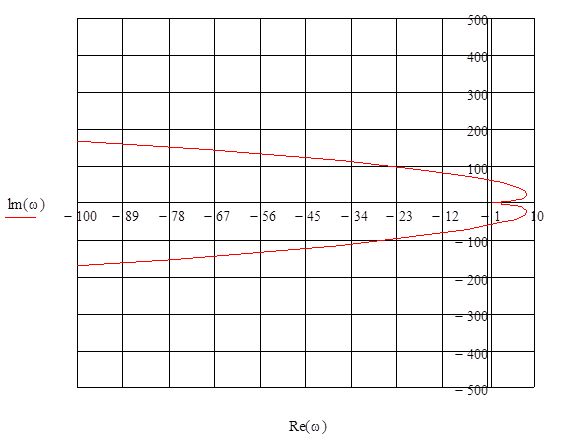
Рисунок 6
АФХ системы
5 Весовая и переходная функции разомкнутой системы
Переходная характеристика в операторном виде:
q(p)
= ![]() ;
;
q(p)
= 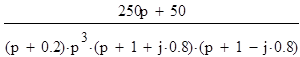 ;
;
Выполнив обратное преобразование Лапласа, получаем переходную характеристику во временной области:
q(t)=
![]() ;
;
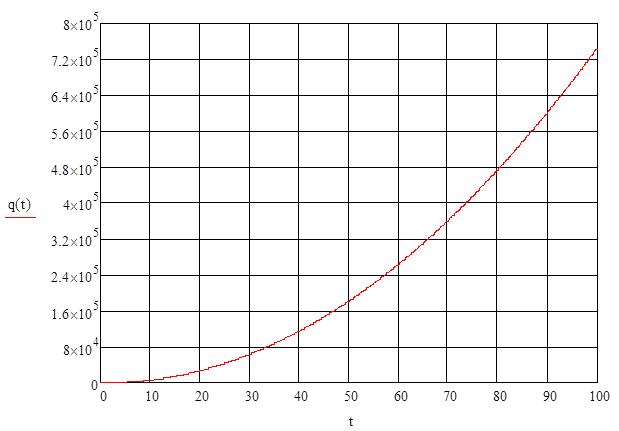
Рисунок 6
Переходная характеристика системы
Весовая функция системы определяется как производная переходной характеристики по времени.
w(t)=![]() ;
;
w(t)=
![]() ;
;
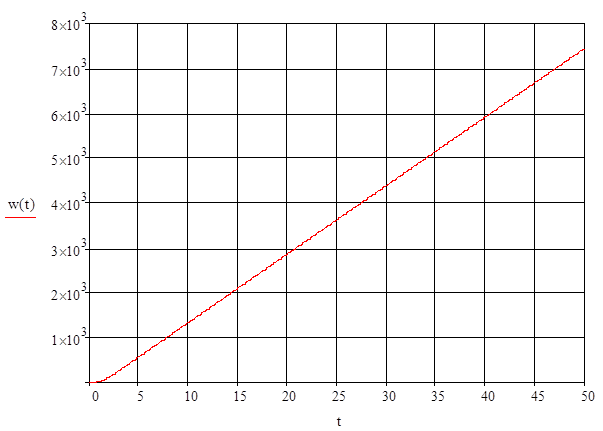
Рисунок 7
Весовая функция системы
6 Анализ устойчивости работы замкнутой системы
А) по критерию Рауса-Гурвица
Формулировка критерия Рауса: для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса имели один и тот же знак, т.е. при а0>0 были положительными с11= а0>0, с12=a1>0, с13>0,..., c1,n+1>0.
Формулировка критерия Гурвица: для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы все определители Гурвица имели знаки, одинаковые со знаком первого коэффициента характеристического уравнения а0, т.е. при а0>0 были положительными.
Характеристическое уравнение для замкнутой системы автоматического управления имеет вид:
![]() ;
;
![]() ;
;
![]() ;
;
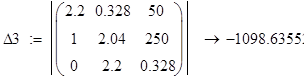 ;
;
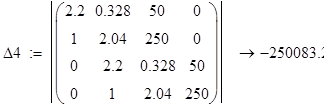 ;
;
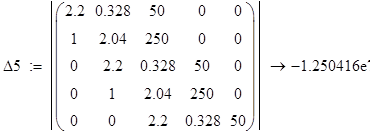 ;
;
Т.к три определителя матрицы отрицательны система не устойчива.
Б) Критерий Михайлова
Формулировка критерия: для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы кривая (годограф) Михайлова при изменении частоты ω от 0 до ∞, начинаясь при ω=0 на вещественной положительной полуоси, обходила только против часовой стрелки последовательно п квадрантов координатной плоскости, где n - порядок характеристического уравнения.
Запишем характеристическое уравнение замкнутой системы:
![]() ;
;
Полагая p=jω, и выделяем у этого уравнения действительную и мнимую части:
![]() ;
;
Реальная часть:
![]() ;
;
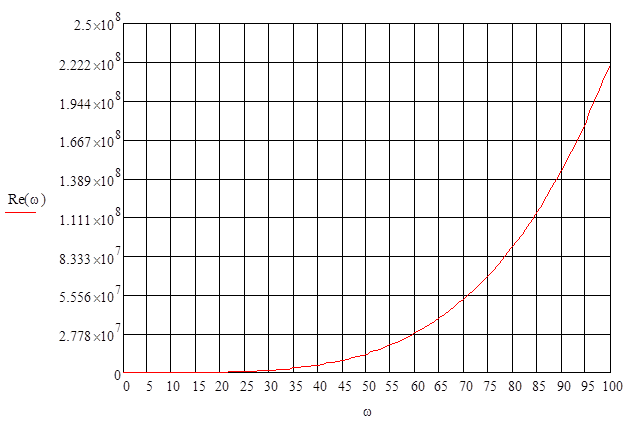
Рисунок 8
График действительной составляющей
Мнимая составляющая:
![]() ;
;
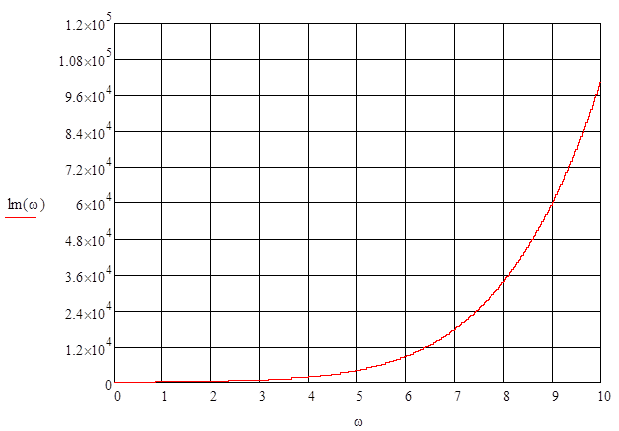
Рисунок 9
График мнимой составляющей
Годограф Михайлова:
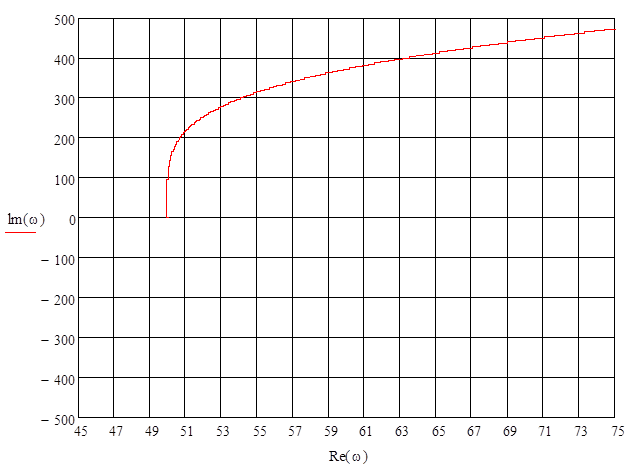
Рисунок 10
Годограф Михайлова
Видно, что при изменении частоты от 0 до ∞, годограф Михайлова находится только в первой четверти, следовательно, система неустойчива.
В) Анализ устойчивости по критерию Найквиста
Формулировка критерия: для того чтобы замкнутая система ∞автоматического управления была устойчива, необходимо и достаточно, чтобы АФХ разомкнутой системы при изменении частоты со от 0 до ∞ не охватывала точку с координатами (-1, j0).
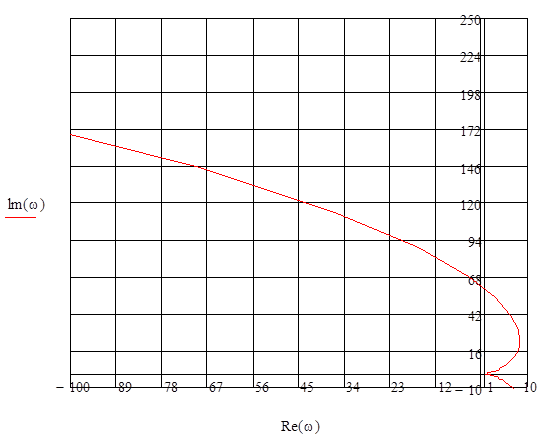
Рисунок 11
АФХ системы
Как видно, АФХ разомкнутой системы при изменение частоты от 0 до ∞ охватывает точку с координатами (-1;j0), а следовательно система не устойчива.
7 ЛAЧXи ЛФЧХ, асимптотическая ЛАЧХ
А) Анализ устойчивости замкнутой системы по ЛАЧХ и ЛФЧХДля того чтобы проанализировать устойчивость системы с помощью логарифмических частотных характеристик необходимо определить частоты среза и резонансные частоты. Если частота среза больше значения резонансной частоты система будет являться неустойчивой.
Построим ЛАЧХ:
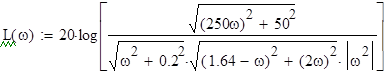
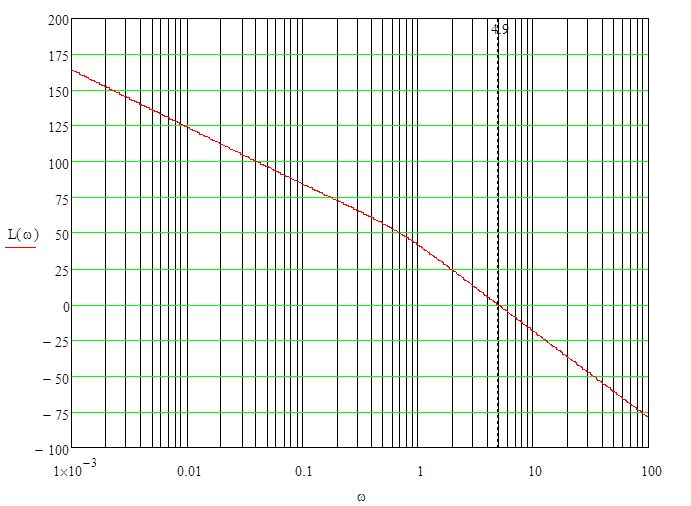
Рисунок 12
ЛАЧХ системы
По графику ЛАЧХ на уровне L(w)=0, найдем частоту среза, ωср=4,9.
![]() ;
;
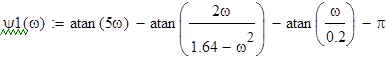 ;
;
![]() ;
;
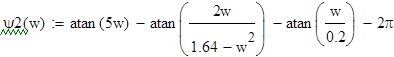 ;
;
Построим ЛФЧХ:
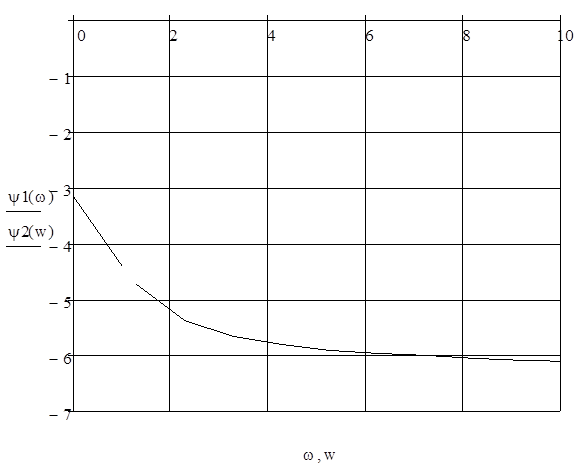
Рисунок 13
ФЧХ системы
Из графика ЛФЧХ на уровне –π найдем резонансную частоту: ωр=0.
ωр˂ ωср, следовательно система неустойчива.
Б)Асимптотическая ЛАЧХ:
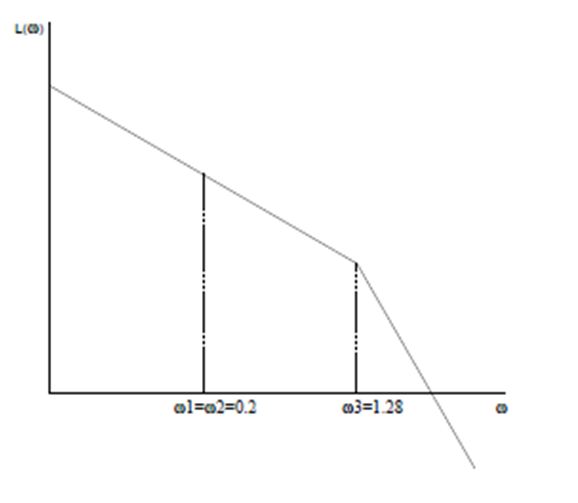
Рисунок 14
Асимптотическая ЛАЧХ системы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.