




Федеральное агентство по образованию РФ
Лабораторная работа № 4
ОПРЕДЕЛЕНИЕ ТОЧНОСТИ
МЕТОДОМ CТАТИСТИЧЕСКИХ ИСПЫТАНИЙ
Проверил:
1. Цель работы: изучение метода статистических испытаний.
2. Исходные данные для расчета
Особенность метода статистических испытаний в том, что он требует применения большого количества опытов или вычислений. Теоретической основой метода является теорема Бернулли, в соответствии с которой при увеличении числа опытов частота появления события стремится к его вероятности.
На
основе теоремы Бернулли при достаточно большом числе опытов за вероятность
попадания параметра в пределы поля допуска, т.е. ![]() , можно
принять частоту (статистическую вероятность), определяемую по формуле:
, можно
принять частоту (статистическую вероятность), определяемую по формуле:
![]() , (1)
, (1)
где m – число попаданий параметра N в заданный интервал; n – общее количество вычислений.
Ошибка ε в определении искомой вероятности Pпо частоте Р* в зависимости от доверительной вероятности γ и числа вычислений п находится по формуле:
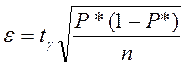 (2)
(2)
где
![]() -
параметр распределения Стьюдента.
-
параметр распределения Стьюдента.
Для равномерного закона случайные числа ui, равномерно распределенные в интервале от а до b, получают при помощи линейного преобразования:
![]() , (3)
, (3)
где
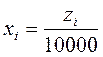 , а – минимальное значение величины,
b – максимальное значение величины.
, а – минимальное значение величины,
b – максимальное значение величины.
Для закона нормального распределения с параметрами ![]() ,
, ![]() ,
случайные числа ui получают при помощи линейного преобразования:
,
случайные числа ui получают при помощи линейного преобразования:
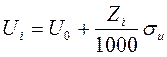 , (4)
, (4)
где
U0 –
номинальное значение величины, ![]() - стандарт, рассчитываемый по правилу трех
сигм:
- стандарт, рассчитываемый по правилу трех
сигм:
![]() , (5)
, (5)
где
![]() - половина поля допуска.
- половина поля допуска.
3. Расчет цилиндрической жесткости пластины
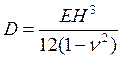 (6)
(6)
![]() Н/м2 - нормальный закон распределения
Н/м2 - нормальный закон распределения
![]() м - равномерный закон распределения
м - равномерный закон распределения
![]() -
нормальный закон распределения
-
нормальный закон распределения
![]()
Расчет номинального значения величины по формуле (6):
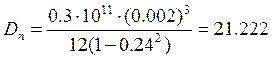 Н·м
Н·м
Допуск составляет ![]() , где 3% от номинального значения:
, где 3% от номинального значения: ![]() Н·м
Н·м
Тогда
![]() .
.
Для расчета необходимо просчитать для каждого параметра необходимые данные:
Для
![]() Н/м2
Н/м2
![]() Н/м2
Н/м2
Тогда из выражения (5):
![]() Н/м2
Н/м2
Для
![]() м
м
![]() м
м
![]() м
м
![]() м
м
Для
![]()
![]()
Тогда из выражения (5):
![]()
Необходимо провести 20 расчетов.
Пример расчета случайной величины для модуля упругости Е по формуле (4):
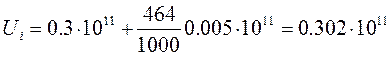 Н/м2
Н/м2
Пример расчета случайной величины для толщины пластины Н по формуле (3):
![]() м
м
Пример
расчета случайной величины для коэффициента Пуассона ![]() по
формуле (4):
по
формуле (4):
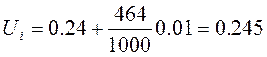
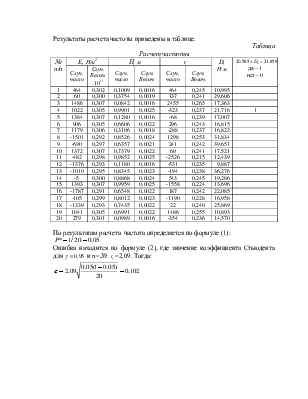
Результаты расчета частоты приведены в таблице.
Таблица
Расчет частоты
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.