Определение точности методом cтатистических испытаний, страница 2

№ n/n	E, Н/м2		Н, м				D, Н·м	да – 1 нет – 0
	Случ. число	Случ. Велич.	Случ. число	Случ. Велич.	Случ. число	Случ. Велич.
1	464	0,302	0,1009	0,0016	464	0,245	10,995
2	60	0,300	0,3754	0,0019	137	0,241	29,606
3	1486	0,307	0,0842	0,0016	2455	0,265	17,363
4	1022	0,305	0,9901	0,0025	-323	0,237	21,716	1
5	1384	0,307	0,1280	0,0016	-68	0,239	17,007
6	906	0,305	0,6606	0,0022	296	0,243	16,815
7	1179	0,306	0,3106	0,0018	-288	0,237	16,822
8	-1501	0,292	0,8526	0,0024	1298	0,253	31,834
9	-690	0,297	0,6357	0,0021	241	0,242	39,651
10	1372	0,307	0,7379	0,0022	60	0,241	17,521
11	-482	0,298	0,9852	0,0025	-2526	0,215	12,439
12	-1376	0,293	0,1180	0,0016	-531	0,235	9,887
13	-1010	0,295	0,8345	0,0023	-194	0,238	36,276
14	-5	0,300	0,8868	0,0024	543	0,245	19,286
15	1393	0,307	0,9959	0,0025	-1558	0,224	13,696
16	-1787	0,291	0,6548	0,0022	187	0,242	22,085
17	-105	0,299	0,8012	0,0023	-1190	0,228	16,958
18	-1339	0,293	0,7435	0,0022	22	0,240	25,869
19	1041	0,305	0,6991	0,0022	1486	0,255	10,893
20	279	0,301	0,0989	0,0016	-354	0,236	14,570

По результатам расчета  частота определяется по формуле (1):

Ошибка находится по формуле (2), где значение коэффициента Стьюдента для  и п=20: =2,09. Тогда:

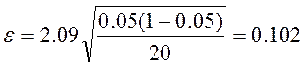
Будем считать, что функциональная зависимость

                                      (1)

задана в аналитическом виде.

Подставляя в зависимость (1) по одному случайному значению , получим одно случайное значение N. Если многократно повторить расчет, подставляя каждый раз новые случайные значения x_i, выбранные в соответствии с их законами распределения, то получим множество значений N. Обработав это статистические данные, можем построить гистограмму и определить закон распределения параметра N.

Ом

Вероятности могут быть найдены по формуле:

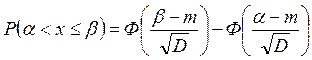
Для резистора R3:

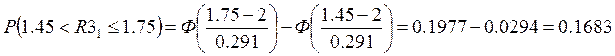
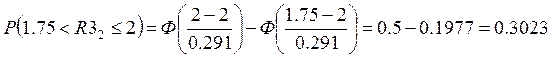
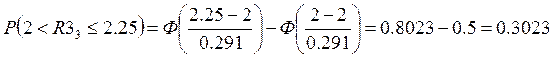
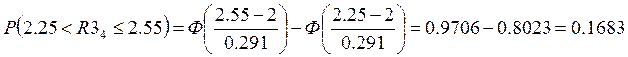
Для резистора R4:

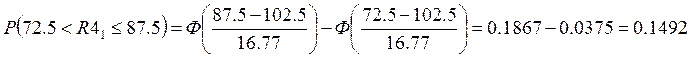
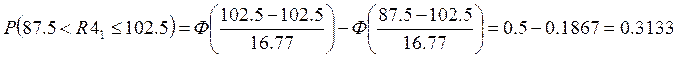
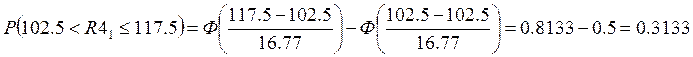
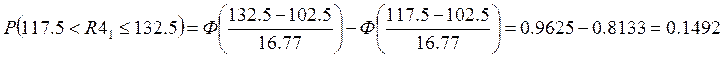
Вероятность того, что схема окажется неработоспособной, выражается так:

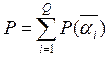,                                           (1)

где Q – число отказных ситуаций.

Вероятность отказных ситуаций находят:

Пример расчета вероятности:

Результаты расчетов вероятностей для отказных ситуаций сведены в таблицу 3.

Таблица 3

Расчет вероятностей для отказных ситуаций

	Uпит = 9,5 В				Uпит = 10 В				Uпит = 10,5 В
	R31	R32	R33	R34	R31	R32	R33	R34	R31	R32	R33	R34
R41	0.0251	-	-	-	-	-	0,0451	-	-	-	0,0451	-
R42	0.0527	0.0947	-	-	-	-	-	-	-	-	-	-
R43	0.0527	0.0947	0,0947	0,0527	0.0527	0.0947	0,0947	0,0527	0.0527	-	-	0,0527
R44	0.0251	0.0451	0,0451	0,0251	0.0251	0.0451	0,0451	0,0251	0.0251	0.0451	0,0451	0,0251

Вероятность отказа по формуле (1) составляет:

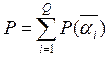
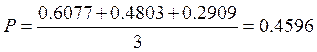
Выводы: