Оценка генеральных характеристик параметра качества по выборочным значениям

Федеральное агентство по образованию Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

Владимирский Государственный университет

Кафедра конструирования и технологии радиоэлектронных средств

Лабораторная работа № 2

«Оценка генеральных характеристик параметра качества по выборочным значениям»

По дисциплине «Математические основы проектирования электронных средств»

Выполнил:

Студент гр. Р-108

Принял:

Владимир 2010

Цель работы: изучение методов оценки генеральных характеристик по выборочным значениям.

Теоретические сведения.

Выборочные  параметры  являются  случайными  величинами.  Их  отклонения  от  генеральных  параметров  (погрешности)  также  случайны.

Оценка  этих  отклонений  носит  вероятностный  характер — можно  лишь  указать  вероятность  той  или  иной  погрешности.  Для  этого  в  математической  статистике  пользуются  доверительными  интервалами  и   доверительными  вероятностями.

Пусть  для  генерального  параметра a получена  из  опыта  несмещенная  оценка  .  Требуется  оценить  возможную  при  этом  ошибку.  Назначим  достаточно  большую  вероятность  ,  такую,  что  событие  с  вероятностью    можно  считать  практически  достоверным,   и  найдем  такое  значение  ,  для  которого

.

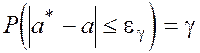При  этом  интервал  практически  возможных  значений  ошибки,  возникающей  при  замене  на , будет  . Большие по абсолютной  величине   ошибки   будут   появляться   только   с   малой   вероятностью , называемой  уровнем   значимости.    Выражение   можно  также  интерпретировать   как  вероятность   того,   что   истинное   значение параметра   лежит  в  пределах

.

Вероятность γ,  называемая   доверительной  вероятностью,  характеризует  надежность  полученной  оценки.  Интервал     называется  доверительным  интервалом.   Границы  интервала  называются  доверительными  границами.   Доверительный  интервал  определяет  точность  оценки.

Величина  доверительного  интервала  зависит  от  доверительной  вероятности,   с  которой  гарантируется  нахождение  параметра    внутри  доверительного  интервала:  чем  больше  величина  γ,  тем  больше  и  величина  ,  т. е.   чем  с  большей  надежностью  хотим  гарантировать  полученный  результат,   тем   в   большем  интервале  значений  он  может  находиться.

Увеличение  числа  опытов  проявляется  в  уменьшении  доверительного  интервала  (повышении  точности  оценки)  при  постоянной  доверительной  вероятности  или  в  повышении  доверительной  вероятности  (повышении  надежности)  при  сохранении  доверительного  интервала.

Доверительный  интервал  для  математического  ожидания     находится    по    неравенству

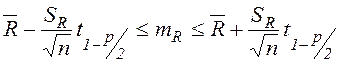, где  , - среднее   арифметическое   и   стандарт    сопротивления   в  выборке;

 - объем  выборки  (задается  преподавателем);

 - уровень  значимости;

 - квантиль  распределения  Стьюдента,  определяемый  по     уровню  значимости    и  числу   степеней   свободы.

Доверительный  интервал  для  дисперсии    при  нормальном  законе  распределения  равен

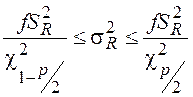, где   - выборочная  дисперсия;

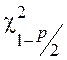,  - квантили распределения Пирсона, определяемые из табл. П2 приложения по уровню значимости  и числу степеней свободы .

Сравнение  дисперсий.   При  обработке  наблюдений  часто  возникает  необходимость  сравнивать  две  или  несколько   выборочных  дисперсий.  Основная  гипотеза,  которая  при  этом  проверяется:  можно  ли  считать  сравниваемые  выборочные  дисперсии  оценками  одной  и  той  же  генеральной  дисперсии.

В  качестве  критерия  значимости   для  сравнения  двух  дисперсий   обычно  используется  критерий  Фишера.  Две  дисперсии  считаются  равными  с  доверительной  вероятностью  ,   если  выполняется  неравенство

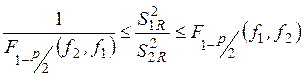, где  выборочные  дисперсии  определяются  по  формуле

   ,   

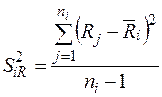 — квантили  распределения  Фишера,  определяемые  из  табл. П5 приложения в  зависимости  от  уровня  значимости  р  и  чисел  степеней  свободы;

 — объемы  выборок,  задаваемые  преподавателем.

При  сравнении  трех  или  более  дисперсий  выборок  одинакового  объема    используют  критерий  Кохрена.   Расхождение  между  дисперсиями   считается   случайным  при  выбранном  уровне  значимости  ,    если

, где   -  квантиль  случайной  величины  при числе суммируемых  дисперсий    и  числе  степеней  свободы  .

Случайная  величина

.

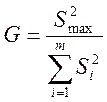При сравнении трех или более дисперсий выборок различного объема