Изучение методики планирования эксперимента, составление математической модели узла РЭА и оптимизировать его параметры

Федеральное агентство по образованию РФ

Государственное образовательное учреждение высшего профессионального образования

Владимирский государственный университет

Факультет радиофизики электроники и медицинской техники

Кафедра конструирования и технологии радиоэлектронных средств

Лабораторная работа №5

“ Разработка математической модели и оптимизация параметров узла РЭА”

                                                                                                Выполнил:

студент группы РЭ-105

Проверил:

Владимир  2007

Цель работы: изучить методику планирования эксперимента, составить математическую модель узла РЭА и оптимизировать его параметры.

Выполнение работы:

Структурная схема экспериментальной установки представлена на рис. 1. Сигнал с генератора 1 и напряжение питания подаются на двухкаскадный УНЧ. Выходное напряжение измеряется при помощи вольтметра.

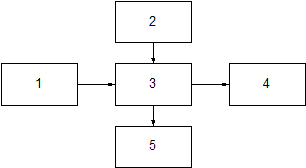
Рис. 1 Структурная схема установки. 1 – генератор ГЗ-34; 2 – источник питания БСП-50; 3 – лабораторный макет УНЧ; 4 – вольтметр ВЗ-6; 5 – авометр АВО-5М1.

Матрица ортогонального планирования задаётся в виде совокупности +1 и -1. Для эксперимента с эффектом взаимодействия матрица имеет вид таблицы 1.

Таблица 1. Матрица планирования

Номер опыта
1	+	–	–	+	+	–	–	+	y1
2	+	–	+	–	–	–	+	+	y2
3	+	+	–	–	–	+	–	+	y3
4	+	+	+	+	+	+	+	+	y4
5	+	–	–	–	+	+	+	–	y5
6	+	–	+	+	–	+	–	–	y6
7	+	+	–	+	–	–	+	–	y7
8	+	+	+	–	+	–	–	–	y8

Так как изменение выходной величины носит случайный характер, то в каждой точке факторного пространства надо проводить m параллельных опытов и результаты усреднять.

Результаты серии опытов представлены в таблице 2.

Таблица 2.

Номер опыта	x0	x1	x2	x3	Выходной параметр U, B
					1	2
1	+	–	–	+	5,3	5,4	5,35	0,0025
2	+	–	+	–	1,5	1,5	1,5	0
3	+	+	–	–	5,2	5,2	5,2	0
4	+	+	+	+	4,9	4,9	4,9	0
5	+	–	–	–	2,8	2,7	2,75	0,0025
6	+	–	+	+	3,2	3,2	3,2	0
7	+	+	–	+	8,7	8,8	8,75	0,0025
8	+	+	+	–	2,5	2,5	2,5	0

Результаты измерений усредняются по формуле:

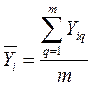
Для первого опыта:.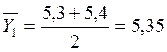

Для второго опыта: 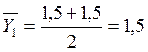. И так далее для всех опытов

Дисперсия среднего значения количественно характеризует ошибку воспроизводимости опытов; определяется по формуле:

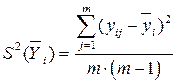, где m – число серий опытов; j – изменяется от 1 до m; i –изменяется от 1 до N.

Для первого опыта: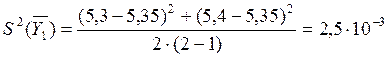

Аналогично рассчитывается и для других опытов.

Проверка однородности дисперсий проводится по критерию Кохрана:

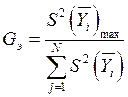
Экспериментальное значение G_э сравнивается с табличным значением G_Т. Если выполняется условие G_э<G_Т, то дисперсии однородны.

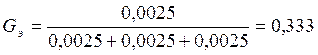
Табличное значение определяется при заданном уровне значимости p=0.05 и числах степеней свободы f₁=m-1=2-1=1, f₂=N=8. Тогда G_Т=0.680.

Так как условие выполняется (0.680<0,333), то дисперсии однородны.

Для трехфакторного эксперимента уравнение регрессии имеет вид:

, где x₁, x₂ и x₃ определяют знак коэффициента регрессии в соответствии с планом эксперимента.

Коэффициент регрессии определяется по формуле:

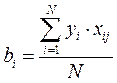, где x_ij определяет знак в соответствии с планом эксперимента, то есть

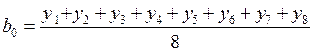
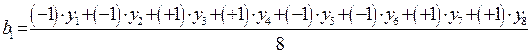 и т.д.

С учетом данных таблиц 1 и 2 получаем:

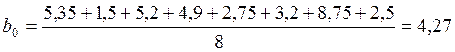
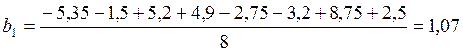
Аналогичным образом рассчитываются коэффициенты b₂, b₃, b₁₂, b₁₃, b₂₃.

Значения коэффициентов регрессии приведены в таблице 3.

Таблица 3.

Коэффициент	b0	b1	b2	b3	b12	b13	b23	b123
Значение	4,27	1,07	-1,24	1,28	-0,39	0,21	-0,26	-0,03

Таким образом, уравнение регрессии имеет вид:

y = 4,27+1,07 x₁ -1,24x₂ +1,28 x₃ - 0,39 x₁x₂ - 0,26x₂ x₃+0,21 x₁x₃ -0,03∙x₁x₂x₃

Значимость коэффициентов регрессии оценивается по критерию Стьюдента.

Во-первых, определяется ошибка эксперимента:

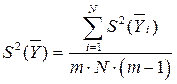
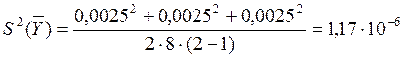
       Дисперсия коэффициента регрессии определяется по формуле:

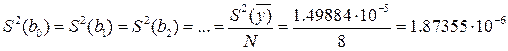
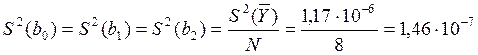
Коэффициент регрессии значим, если

, где t – коэффициент Стьюдента. Для данного эксперимента  t=2.37.

Результаты проверки значимости коэффициентов представлены в таблице 4.

Таблица 4.

Таким образом, все коэффициенты являются значимыми, уравнение регрессии не упрощается.

По полученному уравнению регрессии определяются значения результатов каждого опыта, сравниваются с экспериментальными (см таблицу 5).

Таблица 5.

Проверка адекватности проводится с помощью критерия Фишера. Критерием адекватности является выполнение следующего условия: , где F_p – расчетное значение критерия Фишера:

.

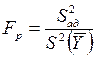Здесь – остаточная дисперсия:

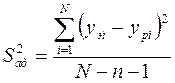, где n – число независимых параметров: d = n; – значение выходного