Проверка гипотезы о нормальном законе распределения статистических данных, страница 2

Для исследуемого случая размах равен 90.

Вместо моды появляется модальный интервал 991-1000, которому соответствует наибольшая частота (30). Данный факт объясняется наличием среди полученных данных пяти значений (наибольшая частота) равных 985 (№№  25, 46, 86, 89, 99) и 989 (№№ 3, 16, 59, 72, 90).

Медиану определим как среднее значение между 50 и 51 элементом нормированного ряда величин измеренных сопротивлений. Эти два числа находятся в интервале 991-1000 и являются соответственно третьим и четвёртым элементом с начала интервала. Число 991 не входит в этот интервал, так как оно было задействовано в предшествующем интервале. Среди измеренных значений есть 4 числа 992, поэтому третьим и четвёртым элементом является число 992, а среднее соответственно тоже 992. И так, медиана равна 992.

Среднее  арифметическое  значение  параметра  приближённо рассчитывается  по формуле

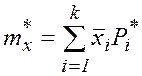, где     k– число  разрядов, - середина  i-го  интервала.

Подставим необходимые данные: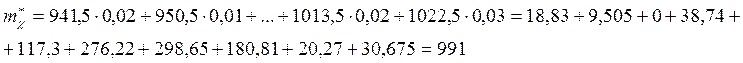  

Статистическая  дисперсия приближенно рассчитывается по формуле

,

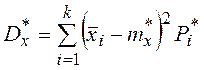Вычислим статистическую дисперсию:

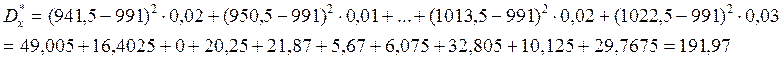
Среднее квадратическое отклонение равно положительному квадратному корню из статистической дисперсии .  Используя значение статистической дисперсии, находим величину квадратического отклонения .

Расчёт теоретической кривой плотности распределения производится по формуле  

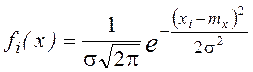, в точках соответствующих границам интервалов.

Далее приведёны таблица значений кривой плотности распределения и  пример расчета для левой границы первого интервала (937): .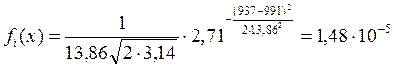

Таблица 3.

Для построения графиков гистограммы и кривой кумулятивной вероятности необходимо произвести некоторые расчеты. Для гистограммы высота прямоугольника находится  по  формуле

.

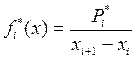Для кумулятивной кривой высота прямоугольника определяется как

,

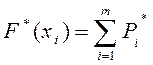где m- число суммируемых частот  до x=x_i .

Например, для гистограммы: для первого интервала 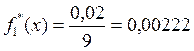 , для второго 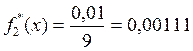, для третьего 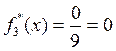. Для кумулятивной кривой , , . Значения, по которым построены гистограмма и кумулятивная прямая приведены в таблице 4.

Таблица 4.