


























Пусть
![]() интегрируема на отрезке
интегрируема на отрезке ![]() для фиксированного
для фиксированного
![]() и любого
и любого ![]() такого,
что
такого,
что ![]() . Выберем точку
. Выберем точку ![]() .
Несобственный интеграл
.
Несобственный интеграл ![]() сходится в том и только том случае,
если сходится несобственный интеграл
сходится в том и только том случае,
если сходится несобственный интеграл ![]() При этом условии имеет место равенство
При этом условии имеет место равенство
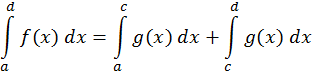
Формула Ньютона-Лейбница для несобственных интегралов. Пусть
![]() -- первообразная непрерывной функции
-- первообразная непрерывной функции ![]() на
интервале (c,d). Предположим, что существуют пределы
на
интервале (c,d). Предположим, что существуют пределы
![]()
Тогда несобственный интеграл ![]() сходится, причём
сходится, причём
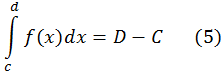
Равенство (5) вытекает из формулы Ньютона-Лейбница для обычных интегралов и соотношений (4).
Пример. Вычислим
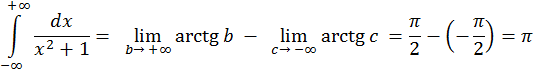
Пусть ![]() на интервале
на интервале ![]() . Тогда
. Тогда
1) если
![]() сходится, то
сходится, то ![]() сходится;
сходится;
2) если
![]() расходится, то
расходится, то ![]() расходится.
расходится.
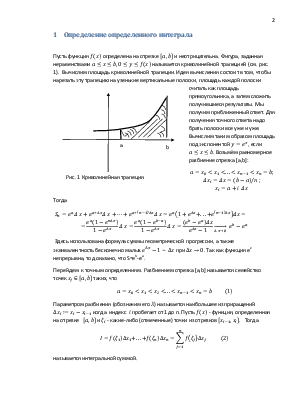
Доказательство. 1) Если ![]() сходится, то существует (конечная)
площадь криволинейной трапеции Т под графиком функции
сходится, то существует (конечная)
площадь криволинейной трапеции Т под графиком функции ![]() .
Криволинейная трапеция под графиком функции
.
Криволинейная трапеция под графиком функции ![]() содержится в Т, следовательно и у нее
площадь также конечна. Тем самым интеграл
содержится в Т, следовательно и у нее
площадь также конечна. Тем самым интеграл ![]() сходится.
сходится.
2). Если бы интеграл ![]() сходился, то и интеграл
сходился, то и интеграл ![]() также бы сходился, согласно
первому утверждению. Это, однако, противоречит условию. Противоречие
показывает, что интеграл
также бы сходился, согласно
первому утверждению. Это, однако, противоречит условию. Противоречие
показывает, что интеграл ![]() должен расходится. □
должен расходится. □
Следствие. Пусть функции ![]() кусочно непрерывны и имеют неотрицательные
значения на пполуинтервале
кусочно непрерывны и имеют неотрицательные
значения на пполуинтервале ![]() . Предположим, что существует предел
. Предположим, что существует предел ![]() причём он отличен от 0. Тогда
интегралы
причём он отличен от 0. Тогда
интегралы ![]() и
и ![]() ведут себя одинаково в смысле
сходимости, т.е. либо оба сходятся, либо оба расходятся.
ведут себя одинаково в смысле
сходимости, т.е. либо оба сходятся, либо оба расходятся.
Аналогичное утверждение имеет место для полуинтервала (c,b].
Предложение об "эталонных" интегралах . Пусть a>0.
1. Интеграл
![]() сходится тогда и только тогда, когда
p>1.
сходится тогда и только тогда, когда
p>1.
2. Интеграл
![]() сходится тогда и только тогда, когда p<1.
сходится тогда и только тогда, когда p<1.
Доказательство. 1. Если ![]() , то
первообразная
, то
первообразная ![]() подинтегральной функции
подинтегральной функции ![]() имеет конечный предел 0 при
имеет конечный предел 0 при ![]() . По
формуле Ньютона-Лейбница для несобственных интегралов, получаем, что интеграл
. По
формуле Ньютона-Лейбница для несобственных интегралов, получаем, что интеграл ![]() сходится и равен
сходится и равен ![]() .
.
Если ![]() , то первообразной подинтегральной функции
служит
, то первообразной подинтегральной функции
служит ![]() , который не имеет конечного предела на
, который не имеет конечного предела на ![]() . Для
. Для ![]() то же
самое можно сказать о первообразной
то же
самое можно сказать о первообразной ![]() .
.
Аналогично, прямыми вычислениями доказывает второе утверждение.
Примеры
1. Интеграл ![]() сходится, так как здесь
сходится, так как здесь ![]() Тогда и интеграл
Тогда и интеграл ![]() будет сходится, ибо на бесконечности имеет
место асимптотическая оценка:
будет сходится, ибо на бесконечности имеет
место асимптотическая оценка:
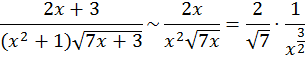
2. Исследуем на сходимость ![]() . Так как
. Так как ![]() при x→ 0, а интеграл
при x→ 0, а интеграл ![]() сходится (здесь
сходится (здесь ![]() -- см. предложение об эталонных
интегралах, пункт 2), то и исходный интеграл сходится.
-- см. предложение об эталонных
интегралах, пункт 2), то и исходный интеграл сходится.
3. Докажем, что интегралы ![]() и
и ![]() сходятся и вычислим их. Имеем
сходятся и вычислим их. Имеем
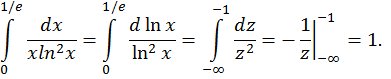
Интеграл ![]() также сходится, ибо занесение под знак
дифференциала
также сходится, ибо занесение под знак
дифференциала ![]() и замена
и замена ![]() превращают его в интеграл
превращают его в интеграл ![]() , который сходится согласно предложению об
эталонных интегралах и равен 1.
, который сходится согласно предложению об
эталонных интегралах и равен 1.
Интегралы ![]() и
и ![]() расходятся, так как такая же замена
приводит их к несобственным эталонным интегралам
расходятся, так как такая же замена
приводит их к несобственным эталонным интегралам ![]() и
и ![]() , с
, с ![]()
Теорема сравнения и ее следствие применимы только к
неотрицательным функциям. Как исследуется на сходимость несобственный
интеграл ![]() в случае функции
в случае функции ![]() , меняющей знак на полуинтервале
, меняющей знак на полуинтервале ![]() Заметим, что если от функции
Заметим, что если от функции ![]() перейти
к ее модулю
перейти
к ее модулю ![]() , то условие неотрицательности будет
соблюдено.
, то условие неотрицательности будет
соблюдено.
Предложение. Если интеграл от модуля функции сходится, то и интеграл от самой функции также сходится.
Доказательство. Итак, нам известно, что интеграл ![]() сходится. Из неравенств
сходится. Из неравенств ![]() следует
следует ![]() (прибавили ко всем частям величину
(прибавили ко всем частям величину ![]() ). Из сходимости
). Из сходимости ![]() вытекает сходимость
вытекает сходимость ![]() (свойство линейности). Тогда по теореме
сравнения получаем, что и интеграл
(свойство линейности). Тогда по теореме
сравнения получаем, что и интеграл ![]() сходится. Разность двух сходящихся
интегралов
сходится. Разность двух сходящихся
интегралов ![]() и
и ![]() дает сходящийся интеграл
дает сходящийся интеграл ![]() , что и требовалось доказать. □
, что и требовалось доказать. □
Определение. Несобственный интеграл ![]() называется абсолютно сходящимся, если
интеграл
называется абсолютно сходящимся, если
интеграл ![]() сходится. В случае, когда несобственный
интеграл
сходится. В случае, когда несобственный
интеграл ![]() сходится, но не сходится абсолютно, то
интеграл
сходится, но не сходится абсолютно, то
интеграл ![]() называют условно сходящимся.
называют условно сходящимся.
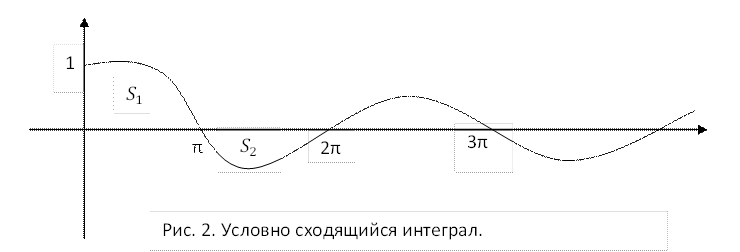
Пример. Интеграл ![]() сходится условно. Обозначим
сходится условно. Обозначим ![]() Геометрический аналог этого утверждения
заключается в том, что суммарная площадь
Геометрический аналог этого утверждения
заключается в том, что суммарная площадь ![]() равна бесконечности, хотя
знакочередующийся ряд
равна бесконечности, хотя
знакочередующийся ряд ![]() сходится (см. рис. 2).
сходится (см. рис. 2).
Действительно, для ε >0 имеем:
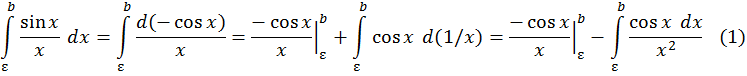
Так как ![]() и интеграл
и интеграл ![]() сходится, то при
сходится, то при ![]() правая
часть в (1) имеет предел. Следовательно, и левая часть
правая
часть в (1) имеет предел. Следовательно, и левая часть ![]() имеет предел при
имеет предел при ![]() Итак,
интеграл
Итак,
интеграл ![]() сходится. Точка 0 есть устранимая
особенность функции
сходится. Точка 0 есть устранимая
особенность функции ![]() в силу первого замечательного предела.
Доопределяя эту функцию в нуле единицей, получаем непрерывную функцию
в силу первого замечательного предела.
Доопределяя эту функцию в нуле единицей, получаем непрерывную функцию
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.