Элементы теории алгоритмов. Абстрактный алфавит, алфавитный оператор, массовость, результативность, страница 5

Алгоритмы, которые применяют на практике, можно разбить на два класса: детерминированные и недетерминированные. Как отмечалось, детерминированные алгоритмы состоят из операций, результат каждой из которых определен однозначно. Если алгоритм содержит операции, результат выполнения которых неоднозначен, то он относится к классу недетерминированных алгоритмов.

Задачей на допустимость считается задача определения хотя бы одного возможного решения. Задачей на оптимальность считается задача определения допустимого решения, дающего экстремум целевой функции рассматриваемой системы. Множество всех задач на допустимость, которые могут быть решены на основе детерминированного алгоритма за полиномиальное время, относится к подклассу полиномиальных алгоритмов и обозначается Р. Подклассом NP называется множество всех задач на допустимость, которые могут быть решены с помощью недетерминированного алгоритма за полиномиальное время. В NP входят задачи, вообще говоря, решаемые, но для которых сейчас известны только детерминированные алгоритмы с экспоненциальным временем решения. Так как детерминированные алгоритмы являются частным случаем недетерминированных алгоритмов, то считают, что

Одна из основных проблем в САПР заключается в исключении или уменьшении перебора при решении конструкторских и технологических задач, т. е, в поиске решения без перебора всех или почти всех вариантов решений. Известно, что задача перебора решается эффективно, если  является полиномиальной функцией. Считают, что задача перебора А сводится к задаче перебора В, если метод решения задачи В можно преобразовать в метод решения задачи А. Сводимость называется полиномиальной, если преобразование выполняется за полиномиальное время, в противном случае сводимость экспоненциальная.

При рассмотрении практических алгоритмов САПР часто встречается следующее: если некоторая задача может быть решена эффективно, то и много других задач, сводимых к ней, могут быть решены эффективно. Пусть имеются две задачи конструирования ЭВА, например компоновка (К) и трассировка (Г). Говорят, что задача К сводится к задаче Т, если задачу К можно решить за полиномиальное время на основе полиномиального детерминированного алгоритма решения задачи Т.

В последние годы было показано, что некоторое подмножество задач в классе NP имеет замечательное свойство: все проблемы в NP эффективно сводятся к этому подмножеству. Это подмножество задач в NP называется ^VP-полным и обозначается NPC. Причем Тогда если некоторая из задач в NPC будет иметь эффективный алгоритм, то и каждая задача в NPC может быть решена эффективно.

Неформально недетерминированным алгоритмом считают, например, такой алгоритм, который способен сделать произвольный выбор между двумя альтернативными путями решения. К NΡ-полным задачам относят задачи размещения штейнеровых точек на плоскости, определения изоморфизма и изоморфного вложения графов, коммивояжера, раскраски графов, определения планарности графов, покрытия множества вершин графов, определения гамильтоновых циклов и максимальных разрезов в графах, трассировки и др.

Рассмотрение практических алгоритмов САПР показывает, что все операции, выполняемые в алгоритмах, распадаются на две группы, которые называются арифметическими и логическими. Арифметические операции выполняют непосредственное преобразование информации, а логические определяют последовательность выполнения арифметических. В этой связи необходимо использование более универсальных логических элементарных операций. Рассмотрим ниже алгоритмы Ван-Хао, Маркова и Ляпунова.

Операторный алгоритм Ван-Хао задается последовательностью приказов специального вида. Каждый приказ имеет определенный номер и указания, какую операцию необходимо выполнять над заданным объектом и с каким номером следует далее выполнить действия над результатом данной операции. В общем виде приказ запишется как

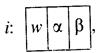
где i—номер приказа; w—элементарная операция над объектом;

α, β—номера некоторых приказов.

Выполнить приказ над числом χ в операторном алгоритме—значит найти число w(x) и затем перейти к выполнению над w(x) приказа с номером а. Если w(x) не определено, то перейти к выполнению над числом χ приказа с номером β. Заключительному состоянию в операторных алгоритмах соответствует приказ