Элементы теории алгоритмов. Абстрактный алфавит, алфавитный оператор, массовость, результативность, страница 3

Процедуру, которая прямо или косвенно обращается к себе, называют рекурсивной. Рекурсия—способ задания функции, когда значение определяемой функции для произвольных значений аргумента выражается известным образом через значения определяемой функции для меньших значений аргументов.

Численные функции, значения которых можно установить на основе некоторого алгоритма, называются вычислимыми. Совокупность численных функций, совпадающих с совокупностью всех вычислимых функций, считают совокупностью рекурсивных функций (РФ). Существует гипотеза о том. что класс РФ гождествен классу всюду определенных вычислимых функций.

Использование РФ в теории алгоритмов основано на идеях нумерации слов в произвольном алфавите последовательными натуральными числами. После нумерации слов произвольный АО превращается в функцию y=f(х). где аргумент x и функция y принимают неотрицательные целочисленные значения. Такие функции называют арифметическими (АФ). Выделяют элементарные АФ:

тождественно равные нулю;

тождественные, повторяющие значения своих аргументов;

непосредственного следования типа f(x)=x+1. На основе перечисленных функций с помощью конструктивных приемов можно строить все более и более сложные АФ. В теории ΛΦ используются операции суперпозиции, примитивной рекурсии и наименьшего корня.

Для решения той или иной задачи ее часто разбивают на части, определяют их решения, а затем из них получают решение всей задачи. Этот прием, если применять его рекурсивно, в основном приводит к эффективному решению задачи, подзадачи которой представляют собой её меньшие версии.

Концепции алгоритмов были впервые описаны в математических терминах в 30-е годы, когда велись поиски условий, с помощью которых доказательство математических теорем может генерироваться автоматически посредством механического процесса. Математик Тьюринг был одним из основателей в развитии этой области. Машина Тьюринга (МТ) была описана как автоматическая с бесконечной длиной лента с отмеченными квадратами и считывающей головкой. Машина была способна только на четыре действия:

движение ленты на один квадрат;

размещение метки в квадрате;

стирание метки, представленной в квадрате; конец вычисления.

Модель МТ показана на рис. 1.2. Она состоит из информационной ленты, представляющей собой бесконечную память машины. В качестве информационной ленты можно использовать магнитную или бумажную ленту, разделенную на квадраты (ячейки). В каждой ячейке можно поместить один любой символ конечного алфавита   Машина Тьюринга имеет считывающую головку, способную просматривать содержимое ячеек. Вдоль нее лента перемещается в обе стороны так, чтобы в любой рассматриваемый момент головка находилась в одной ячейке ленты. Кроме того, МТ имеет устройство управления, которое в рассматриваемый

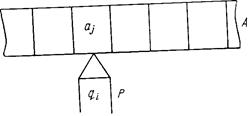момент находится в одном из состояний Q={q₁ , q₂ ..., q_n}· Состояние устройства управления называют внутренним состоянием МТ. Одно из состояний является заключительным и управляет окончанием работы МТ. Машина Тьюринга может сдвигать ленту на одну ячейку вправо или влево, оставляя содержимое ячеек неизменным, или может изменять состояние воспринимаемой ячейки, оставляя ленту неподвижной. Следовательно, МТ состоит из внутренней (конечное множество состояний) и внешней (лента) памяти. Данные МТ—это слова в абстрактном алфавите ленты. На ленте МТ записывают исходные данные и конечные результаты.

Существует тезис Тьюринга: «Всякий алгоритм может быть реализован машиной Тьюринга». Показано, что если задачи не могут быть решены на МТ, то они не могут быть решены ни на какой другой автоматической ЭВМ, т. е. это проблемы, для которых алгоритмы не могут быть составлены даже в принципе. Следовательно, невозможность построения МТ означает отсутствие алгоритма решения данной задачи. Следует отметить, что речь идет об отсутствии алгоритма, решающего всю данную задачу, что не исключает возможность решения этой задачи в частных случаях различными методами.