Нахождение оптимальных параметров и экстремумов целевой функции методом линейного программирования

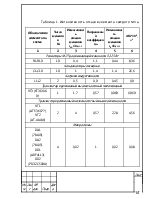
Содержание

Введение……………………………………………………………..………………………………………………………2

1  Рассчитать допуски замыкающего звена……………………………………………………..3

2  Рассчитать вероятность безотказной работы схемы конвертера……...8

3  Нахождение оптимальных параметров и экстремумов целевой функции методом линейного программирования………………………………………………..13

Список литературы……………………………………………….……………………………………………….17

Введение

На современном этапе развития электронной техники все большее значение приобретают теоретические подходы при создании ЭС различной степени сложности, т.к. позволяют быстрее и с лучшим качеством создавать современную аппаратуру общего и специального назначения. Поэтому знать теоретические основы создания ЭС необходимо, т.к. вопросы конструирования, разработки технологии и обеспечения надежности РЭС имеют большое значение в настоящее время.

При высокой сложности аппаратуры использование удовлетворительных конструкторских и технологических решений уже не представляется возможным, и необходимо искать решения, близкие к оптимальным. Установить такие решения опытным путем практически невозможно; они могут быть получены лишь на основании теоретического анализа.

По своей математической постановке технологические задачи схожи с конструкторским0и, и для их решения используют те же математические методы, что и для решения конструкторских задач.

С развитием микроэлектроники сложность процесса создания ЭС усложняется прежде всего в теоретическом плане, поэтому необходимо знать математические методы, используемые для анализа, синтеза и оптимизации процессов конструирования и технологии производства ЭС с целью повышения его качества.

1  рассчитать допуски замыкающего звена

Задание: определить допуски замыкающего звена детали методами предельных отклонений и вероятностным при следующих исходных данных (риунок 2, А1 = 80_-0,4; А2 = 40_-0,2; А3 = 20 ± 0,1; а_i = а_j = 0,2; К_i = К_j = 1,2). Сравнить полученные результаты.

Допуск – это предельное значение параметра ограничивающеепогрешности.

Вначале составляется размерная цепь. Размерная цепь – совокупность расположенных по замкнотому контуру разных положений поверхности деталей или деталей в узле.

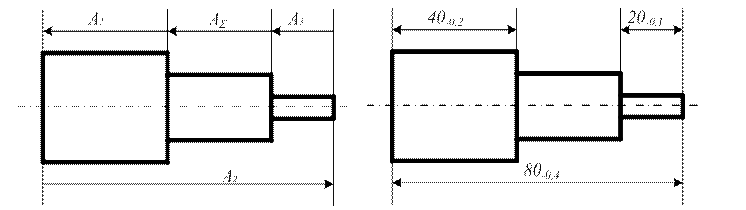
Рисунок 1. – Размерная цепь.

Размеры в размерной цепи называют звеньями. Звенья могут быть увеличивающие и уменьшающие. Увеличивающее звено - это звено, при увеличении которого увеличивается замыкающее звено (A₁). Уменьшающее звено – это звено, с увеличением которого уменьшающее звено (А₂, А₃). Замыкающим звеном является А_Σ.

Существует два метода расчета размерных цепей:

- метод предельных отклонений;

- вероятностный метод.

;                                     (1)

где А_0Σ - номинальное значение размера;

E(ΔА_S) - отклонение середины поля допуска от номинального значения;

d(ΔА_S) - половина поля допуска.

А_0Σ = А₁ – А₂ – А₃ = 80 – 40 – 20 = 20;

Отклонение середины поля допуска от номинального значения:

Е(А₁) = -0,2;

Е(А₂) = -0,1;

Е(А₁) = 0.

Половина поля допуска:

δ(А₁) = 0,2;

δ(А₁) = 0,1;

δ(А₁) = 0,1.

1.1 МЕТОД ПРЕДЕЛЬНЫХ ОТКЛОНЕНИЙ

Отклонение середины поля допуска от номинального значения:

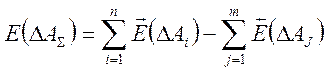;                       (2)

гдеn – количество увеличивающих звеньев;

m – количество уменьшающих звеньев;

→ - принадлежность к увеличивающему звену;

← - принадлежность к уменьшающему звену.

.

Половина поля допуска:

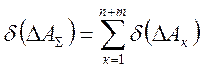;                                         (3)

где n+m – общее количество составляющих звеньев.

.

Предельное отклонение замыкающего звена по данному методу:

.

1.2 ВЕРОЯТНОСТНЫЙ МЕТОД

Отклонение середины поля допуска от номинального значения:

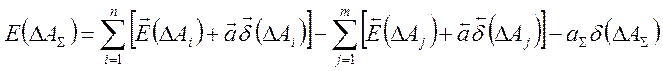;   (4)

гдеа_i, a_j – коэффициент относительности ассиметрии (а= а_i =а_j =0,2);

а_Σ – коэффициент относительности ассиметрии для замыкающего звена.

Условие (а_Σ = 0) не выполняется, тогда коэффициент рассчитывается по полуэмперической формуле:

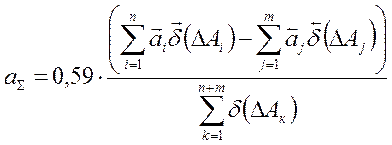;                      (5)

.

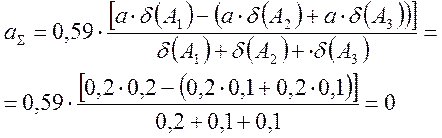
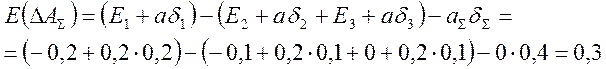Половина поля допуска:

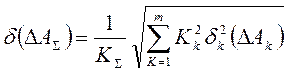;                                     (6)

гдеК_iк – коэффициент относительного рассеивания (К = К_iк = 1,2);

а_Σ – коэффициент относительного рассеивания для замыкающего звена.

Условие (К_Σ = 1) не выполняется, тогда коэффициент рассчитывается по полуэмперической формуле:

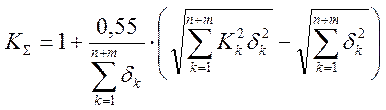;                       (7)

.

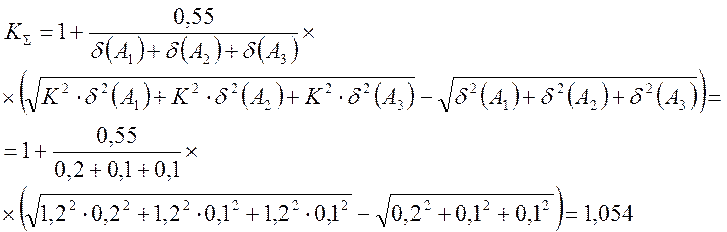
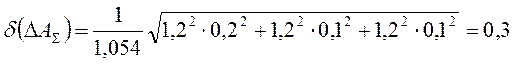Предельное отклонение замыкающего звена по данному методу: