Расчет и выбор магистрали. Расчёт потерь напора на каждом участке магистрали. Определение высоты башни. Расчёт ответвлений

Санкт-Петербургский государственный политехнический университет

Инженерно-строительный факультет

Кафедра гидравлики

Задание № 3 по курсу гидравлики

«Расчет длинных трубопроводов»

Выполнил студент гр. 3013/1:                                         Беллендир Н.Э.

Проверил:                                                                       Локтионова Е.А.

Санкт-Петербург

2011г

ОГЛАВЛЕНИЕ

1.     ТРУБОПРОВОД №1. 3

1.1.        Расчет и Выбор магистрали. 3

1.2.        Расчёт потерь напора на каждом участке магистрали. 4

1.4.        Построение пьезометрической  линии Р-Р для магистрали 1-2-3-4. 5

1.5.        Определение высоты башни. 7

1.6.        Расчёт ответвлений. 7

2.     ТРУБОПРОВОД №2. 10

2.1.        Определение расходов Q_Cmax ,Q_Imax ,Q_IImax 10

2.2.        Построение графиков зависимости расходов Q_I =f(Q_c) и Q_II =f(Q_c) 12

2.3.        Построение пьезометрической линии Р-Р при Q^*_C=0,40Q_IImax 15

ЛИТЕРАТУРА.. 17

1.  ТРУБОПРОВОД №1

1.1.  Расчет и выбор магистрали

Сначала необходимо выбрать магистраль. Выбор магистрали производят, исходя из трех пунктов:

1.  Определяем наиболее длинную линию

Для этого необходимо сложить длины отдельных труб и выбрать наибольшую:

         

;

2.  Находим линию, которая наиболее нагружена расходами

Чтобы выполнить сравнение, достаточно сосчитать расход на каждом из ответвлений:

,

.

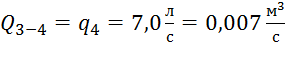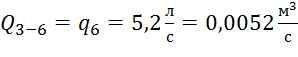В этом же пункте сосчитаем расходы на остальных участках трубопровода, так как дальше они нам понадобятся.

;

;

.

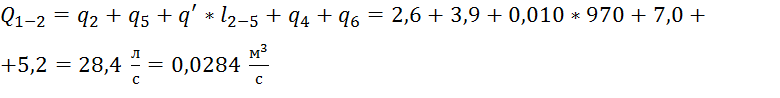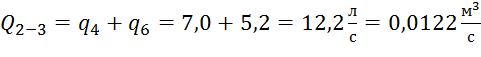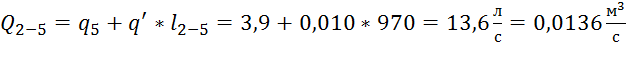3.  Линия, которая подает воду на более высокие отметки.

Таким образом, выбираем магистральную линию .

Расчет магистрали ведется, использую формулы для площади живого сечения:

,

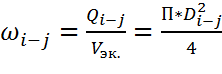где   - расход на рассчитываемом участке,  - диаметр трубы этого участка, а  - экономическая скорость. Экономической скоростью называется скорость воды в трубопроводах, при которой обеспечивается минимальные приведенные затраты на строительство и эксплуатацию внешней системы, и ее значения 1,0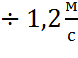. В данном случае 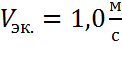. Из вышеприведенной формулы выражаем диаметр:

.

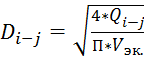По этой формуле находим расчетные диаметры каждого участка магистрали и округляем его до ближайшего стандартного значения по табл. 4.6, стр. 40 [1]. По этой же таблице находим для каждого участка соответствующее диаметру значение модуля расхода .

1.  Участок 1-2:

.

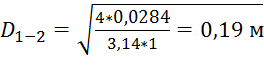По табл. 4.6, стр. 40 [1] ;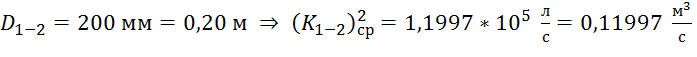

2.  Участок 2-3:

.

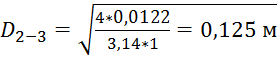По табл. 4.6, стр. 40 [1] ;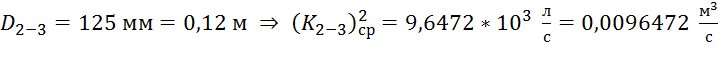

3.   Участок 3-4:

.

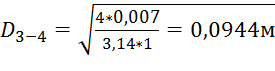По табл. 4.6, стр. 40 [1] .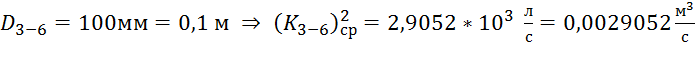

1.2.  Расчёт потерь напора на каждом участке магистрали

Потери напора на каждом участке магистрали рассчитываются по формуле:

.

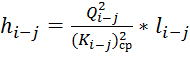1.  Участок 1-2:

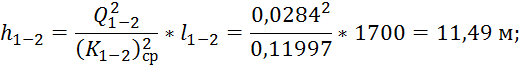
2.  Участок 2-3:

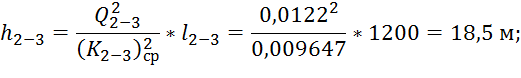
3.  Участок 3-6:

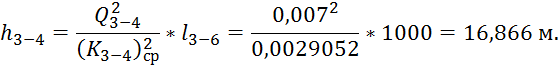
Вычислив все потери напора, найдем отметку , которая соответствует уровню воды в башне:

,

где h – наименьшее допустимое возвышение пьезометрической линии над поверхностью земли в концевых точках сети, равное 3,0 м.

 м.

1.3.  Построение пьезометрической  линии Р-Р для магистрали 1-2-3-4

Используя величины потерь напора на каждом участке, строим пьезометрическую линию Р-Р для магистрали. Построение выполнено на рис. 1.1.

1.4.  Определим высоты башни.

Высоту башни H_б следующим способом:

 =h+ =3,0+0,9=3,9 м;

=+h_3-4 +h_2-3 + h_1-2 =3,9+16,866+18,5+11,49=50,8 м;

Н_б=-=50,8-3,0=47,8 м.

Теперь строим пьезометрическую линию для магистрали (рис. 1).

1.5.  Расчет ответвлений

Ответвление рассчитывается как исходный трубопровод, предполагая, что «высота башни», т.е. пьезометрический напор в начале ответвления задан и равен пьезометрическому напору в магистральной трубе в месте присоединения ответвления.

Ответвление 3-6

Сначала вычислим расчетную потерю напора:

;

;

Из расчета магистрали:

;

Таким образом:

По уже известной формуле определим расчетный модуль расхода:

.

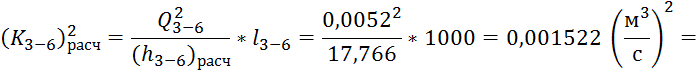
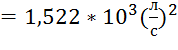По табл. 4.6, стр. 40 [1] находим ближайшее стандартное значение модуля расхода и, соответственно, значение диаметра:

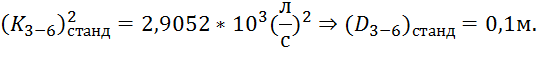
Теперь сосчитаем действительное значение потери напора:

.

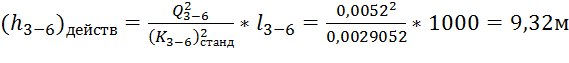На чертеже продольного профиля ответвления 3-6 построим пьезометрические линии с расчетной потерей напора и действительной (рис.2).

Ответвление 2-5

Аналогично вычисляем расчетную потерю напора:

,

где 

       

Найдем модуль расхода:

,

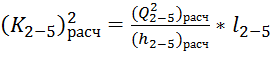где  - расход на этом ответвлении, который вычисляется по формуле:

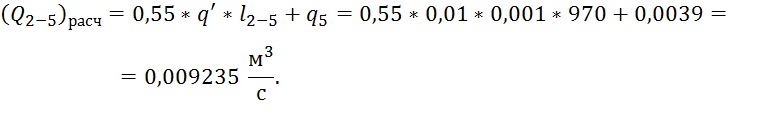
Подставим известные значения в формулу модуля расхода:

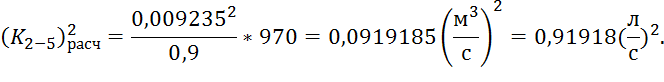
По табл. 4.6, стр. 40 [1] находим ближайшее стандартное значение модуля расхода и, соответственно, значение диаметра:

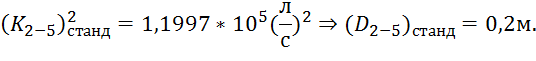
Сосчитаем действительное значение потери напора:

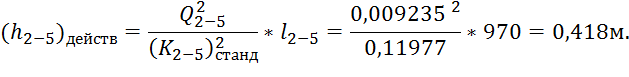
На чертеже продольного профиля ответвления 2-5 построим пьезометрические линии с расчетной потерей напора и действительной (рис.2).

2.  ТРУБОПРОВОД №2

2.1          Определение расходов QCmax ,QImax ,QIImax

Зная диаметр сечения на каждом участке трубопровода, по табл. 4.6, стр. 40 [3] определим значение квадрата модуля расхода для каждого участка:

К₁² =9,647×10³ (л/с)²

К₂² =9,647×10³ (л/с)²

К₃² =2,9052×10³ (л/с)²

К₄² =2,9052×10³ (л/с)²

Составим систему уравнений для трубопровода. Для первых четырёх уравнений воспользуемся формулой (1.4):

1)  ;

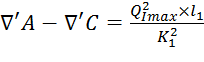2)  ;

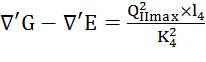3)  ;

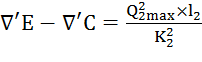4)  ;

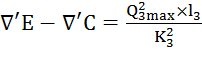5)  ;

6)  .

В этой системе:

Подставим в систему известные численные значения и решим её относительно неизвестных Q_Imax, Q_IImax, Q_Cmax, Q_2max, Q_3max, E:

1)  ;

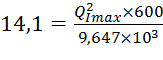2)  ;

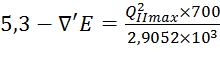3)  ;

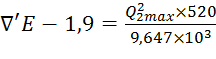4)  ;

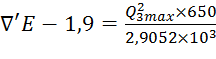5)  ;

6)  .

Из уравнения (1) найдём Q_Imax:

.

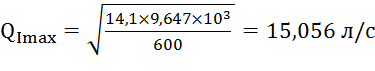Из уравнений (3) и (4) найдём соотношение между Q_2max и Q_3max:

Q²_2max =4,161 Q²_3max  =>  Q_2max =2,04 Q_3max.

Из уравнений (3) и (4) выразим значения Q_2max, Q_3max через E:

;

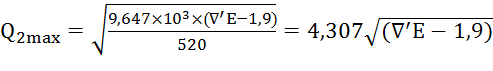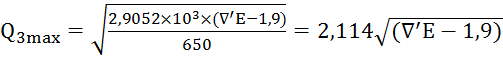. 4,468996

Используя уравнение (5), получим:

4,468996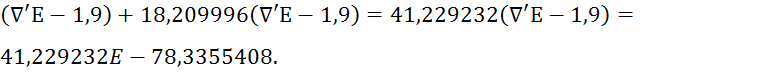

Из уравнения (2):

.

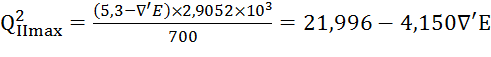Приравняем результаты двух последних выражений и найдём :

;

;

.

Найдём Q_2max и Q_3max, используя уравнения (3) и (4):

;

.

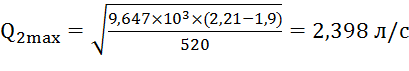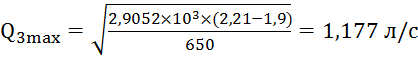Подставляем эти значения в уравнение (5):

.

Из уравнения (6) находим Q_Cmax:

.

Решения системы:

Q_Imax = л/с;

Q_IImax =3,575 л/с;

Q_Cmax =16,631 л/с;

Q_2max =2,398 л/с;

Q_3max =1,177 л/с;

E=2,21 м.

Для проверки правильности решений системы подставим найденные значения в уравнения (2), (3) ,(4) и (5):

;

 ;

 ;

 .

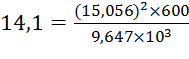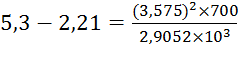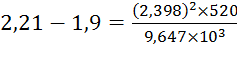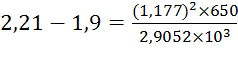2.2.      Построение графиков зависимости расходов                              Q_I =f(Q_c) и Q_II =f(Q_c)

Графики зависимости расходов Q_I =f(Q_c) и Q_II =f(Q_c) строим по трём точкам.

Точка 1 – кран С полностью открыт:

Q_I = Q_Imax =15,056 л/с;

Q_II = Q_IImax =3,575 л/с;

Q_C = Q_Cmax =16,631 л/с.

Точка 2 – кран С полностью закрыт:

Q_C =0  =>  Q_I =Q_II =Q.

Составим систему для данного случая:

1)  ;

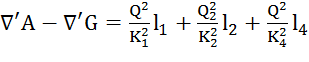2)  ;

3)  .

Уравнение (3) получаем из уравнений (3) и (4) системы в п. 2.1.

Решаем систему. Подставляем уравнение (3) в уравнение (2):

Q=Q₂ +0,663Q₂ =1,663Q₂.

Далее подставляем это значение Q и все известные численные значения в уравнение (1) и получаем:

10,5= .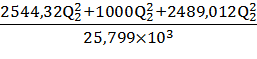

Из этого равенства находим Q₂:

.

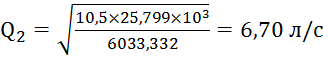Используя уравнение (3) находим Q₃:

Q₃ =0,663Q₂ =0,663×6,70=4,44 л/с.

Подставляя найденные значения Q₂ и Q₃ в уравнение (2) находим Q:

Q=Q₂ + Q₃ =6,70+4,44=11,14 л/с.

Точка 3 – бак II нейтрален:

Q_II =0  =>  Q_I =Q_C.

В этом случае потеря напора в трубопроводе будет равна:

;

.

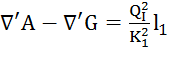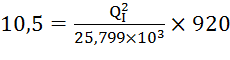Находим Q_I:

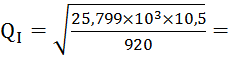  17,16 л/с.

          Для построения искомых графиков нанесём полученные точки на координатную плоскость и соединим. Построение кривых зависимости расходов Q_I =f(Q_c) и Q_II =f(Q_c) выполнено на рис 2.1.

Рис. 2.1.

2.3.    Построение пьезометрической линии Р-Р при Q^*_C=0,40Q_IImax

Q^*_C=0,4Q_IImax =2,61 л/с.

Значения Q^*_I, Q^*_II снимаем с графиков Q_I =f(Q_c) и Q_II =f(Q_c), построенных на рис. 2.1:

Q^*_I =12,4 л/с;

Q^*_II =9,4 л/с.

Вычисляем значения потерь напора на участках l₁  и l₄, используя формулу (1.4):

;

.

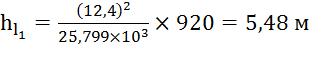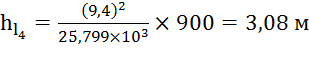Построение пьезометрической линии Р-Р выполнено на рис. 2.2.

Также необходимо выполнить расчет значения потери напора в случае Q_C =0  =>  Q_I =Q_II =Q.

;

.

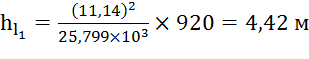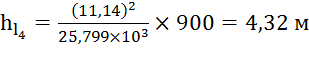На рис. 2.2 выполнено построение пьезометрических линий для случаев:

1)  Q_I = Q_Imax; Q_II = Q_IImax; Q_C = Q_Cmax;

2)  Q_C =0  =>  Q_I =Q_II =Q;

3)  Q_II =0  =>  Q_I =Q_C.

Рис. 2.2.

Литература

1. Механика жидкости и газа (гидравлика): Учебник для вузов / Гиргидов А.Д. СПб.: Изд-во СПбГПУ, 2002. 546 с.

2. Механика жидкости и газа (гидравлика): Метод. рекомендации для выполнения и оформления курсовых и расчетно-графических работ / Е.Н. Кожевникова, Е.А. Локтионова, В.Т. Орлов. СПб.:Изд-во СПбГПУ,2004. 39 с.

3. Механика жидкости и газа (гидравлика). Справочник: Учеб. пособие / Е.Н. Кожевникова, А.И. Лаксберг, Е.А. Локтионова, М.Р. Петриченко. СПб.: Изд-во СПбГПУ, 2007. 90 с.