Лабораторная работа №1
ОСНОВЫ ПРЕОБРАЗОВАНИЯ ФУРЬЕ.
ПРЕОБРАЗОВАНИЕ ФУРЬЕ В MATLAB.
Цель работы:
Задание:
Варианты задания
Построить график стационарного сигнала и с помощью преобразования Фурье определить частотную составляющую:
![]()
1.1. Основные теоретические сведения
При изложении основных теоретических сведений использовались работы [Смоленцев, экспонента]
Математические преобразования применяются к сигналу для того, чтобы получить информацию о нем, недоступную в исходном виде. Наиболее популярным преобразованием сигналов, является преобразование Фурье. Теория вейвлетов в основном является продолжением теории преобразовании Фурье. Поэтому для наилучшего понимания для начала познакомимся с преобразованием Фурье.
Большинство сигналов, встречающихся на практике, представлены во временной области. При отображении такого сигнала на графике по оси абсцисс откладывается время, а по оси ординат амплитуда. Дано представление сигнала называется амплитудно-временным представлением сигнала. Для большинства приложений обработки сигнала это представление не является наилучшим. Во многих случаях наиболее значимая информация скрыта в частотной области сигнала. Частотный спектр есть совокупность частотных (спектральных) компонент, он отображает наличие тех или иных частот в сигнале. В таком представлении сигнала, на оси абсцисс будет откладываться частота, а на оси ординат амплитуда.
Частота измеряется в Герцах [Гц], или в числе периодов в секунду.
На рисунке ниже для примера представлены три синусоиды: 10Гц, 45Гц и 75Гц.
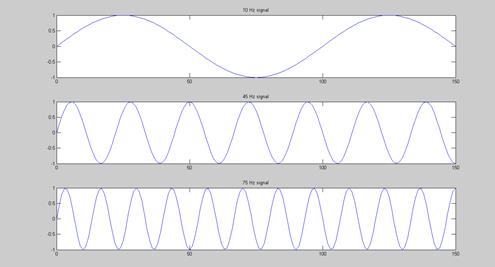
рисунок 1. Синусоиды 10Гц, 45Гц и 75Гц.
Введем некоторые обозначения:
Для числовых рядов ![]() , будем считать, что
, будем считать, что ![]() .
.
 Степенные ряды будем
обозначать
Степенные ряды будем
обозначать 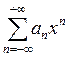 , т.е степени могут быть отрицательными.
, т.е степени могут быть отрицательными.
Для функции ![]() будем считать, что
будем считать, что ![]() .
.
Точка ![]() называется
точкой прикосновения множества
называется
точкой прикосновения множества ![]() , если
любая её окрестность имеет непустое пересечение с этим множеством.
, если
любая её окрестность имеет непустое пересечение с этим множеством.
Замыканием множества ![]() называется совокупность всех точек
прикосновения этого множества.
называется совокупность всех точек
прикосновения этого множества.
Носителем
непрерывной функции ![]() называется замыкание множества
точек
называется замыкание множества
точек ![]() , в которых
, в которых ![]() .
Носитель обозначается символом
.
Носитель обозначается символом ![]() . Если
. Если ![]() находиться на конечном промежутке
находиться на конечном промежутке ![]() , то
, то ![]() называется
функцией с компактным носителем.
называется
функцией с компактным носителем.
Элементарные
гармоники это сигналы вида ![]() и
и ![]() , где
, где ![]() –
амплитуда,
–
амплитуда, ![]() – круговая частота,
– круговая частота, ![]() – начальная фаза.
– начальная фаза.
Преобразованием
Фурье абсолютно интегрируемой на ![]() функции
функции ![]() называется интеграл
называется интеграл
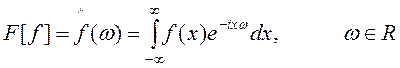 (1)
(1)
Переменная ![]() имеет смысл частоты. Поэтому переход от
имеет смысл частоты. Поэтому переход от ![]() к
к ![]() называют
переходом из пространственной области в частотную.
называют
переходом из пространственной области в частотную.
Обратным преобразованием Фурье называется выражение
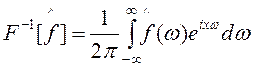 (2)
(2)
в котором интеграл понимается как несобственный в смысле главного значения.
Для того, чтобы проиллюстрировать действие ПФ на функцию рассмотрим примеры.
Импульс прямоугольной формы это колебание определяемое выражением:
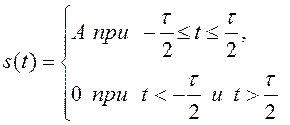 .
.
Применяя формулу (1), находим спектральную плотность
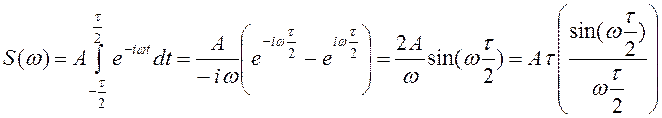 .
.
При ![]()
![]() , заметим, что это площадь импульса. Этот
вывод распространяется на импульс произвольной формы.
, заметим, что это площадь импульса. Этот
вывод распространяется на импульс произвольной формы.
Действительно, из формулы (1) следует , что
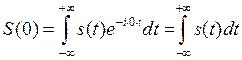
Правая часть этого выражения и есть площадь импульса.
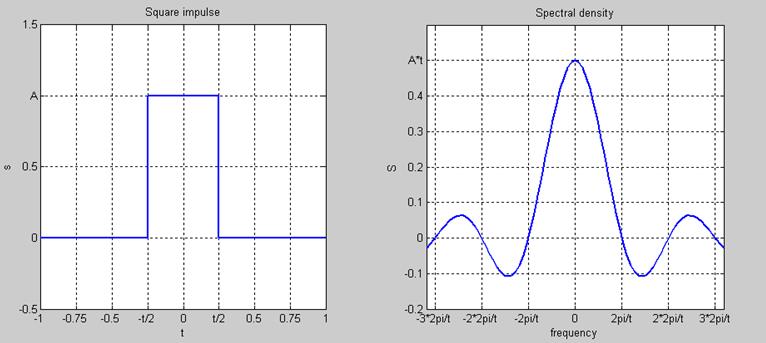
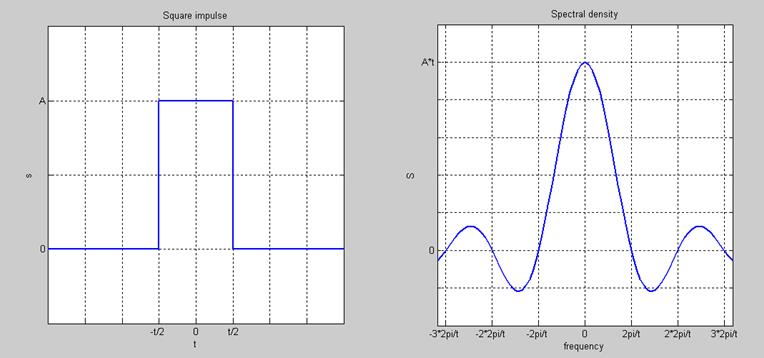
рисунок 2. Импульс прямоугольной формы и его спектральная плотность.
Функция вида 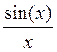 в анализе сигналов встречается довольно
часто и имеет специальное обозначение:
в анализе сигналов встречается довольно
часто и имеет специальное обозначение: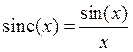 . Она
называется интегральным синусом или функцией отсчетов.
. Она
называется интегральным синусом или функцией отсчетов.
Дискретный сигнал
– это сигнал, аргумент ![]() которого принимает дискретный
ряд значений
которого принимает дискретный
ряд значений ![]() . Тогда сигнал есть
последовательность значений
. Тогда сигнал есть
последовательность значений ![]() . Значения
. Значения ![]() называются отсчетами или выборкой.
называются отсчетами или выборкой.
Дискретизация
непрерывного сигнала ![]() – это замена его
выборкой
– это замена его
выборкой ![]() .
.
Дискретное преобразование Фурье:
Дискретное
преобразование Фурье позволяет преобразовать N отсчетов
сигнала ![]() , в столь ко же спектральных. Для этого
используются формулы:
, в столь ко же спектральных. Для этого
используются формулы:
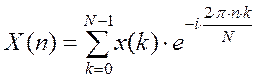 (3)
(3)
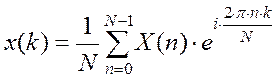 (4)
(4)
В формулах (3)
и (4) нет реальных моментов времени или частоты, а только номера отсчетов во
временной и частотной областях. Чтобы говорить о временном и частотном
масштабах, необходимо знать, с какой частотой брались отсчеты анализируемого
сигнала. Если последовательность представляет собой отсчеты, взятые с частотой
дискретизации ![]() (то есть с интервалом
(то есть с интервалом 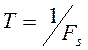 ), то частоты анализа, соответствующие
спектральным отсчетам, полученным в результате вычисления ДПФ, будут
расположены с шагом
), то частоты анализа, соответствующие
спектральным отсчетам, полученным в результате вычисления ДПФ, будут
расположены с шагом 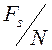 .
.
Первый элемент полученного
вектора соответствует нулевой частоте, последний— частоте ![]() .
.
Замечания:
ü Чтобы расширить полосу анализа, нужно увеличить частоту дискретизации
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.