Пусть в пр-ве задана прямоугольная с-ма координат Охуz и некоторое тело Т удовлетвор. следующ. условиям: 1. тело Т заключено м-ду плоскостями х=а и х=b
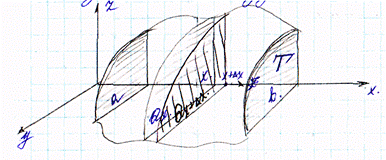
2.
при рассечении тела Т пл.
перпендикулчр. оси Ох в сечении пои любом ![]() получим
квадрируемые плоские сечения Qx
получим
квадрируемые плоские сечения Qx
3.
S сечения Qx является известной непрерывной ф-ей S(x) ![]() для всех х
для всех х
4. проекция любых 2-х сечений Qx1 и Qx2 на плоскость перпендикулярную оси Ох оказываются всегда содержащ. одно в другом.
При
этих условиях тело Т кубируемое т.е.имеет V
который выражается формулой 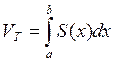 (нужно
показать, что V’(х)=S(x)).
Пусть точка х из [a,b] выбрана произвольно, построим сечение Qx
имеющим площадь S(x). Qx отсекает от тела Т часть V заключено м-ду плоскостями х=а и Qx. V
отсекаемой части тела явл. ф-ей абциссы х (
(нужно
показать, что V’(х)=S(x)).
Пусть точка х из [a,b] выбрана произвольно, построим сечение Qx
имеющим площадь S(x). Qx отсекает от тела Т часть V заключено м-ду плоскостями х=а и Qx. V
отсекаемой части тела явл. ф-ей абциссы х (![]() , V от а
до Qx). V(a)=0 и V(b)=t. С возрастанием х V(x) также
возрастает. Док-ем что V’(х)=S(x). Док-во:
придадим х произвольное приращение
, V от а
до Qx). V(a)=0 и V(b)=t. С возрастанием х V(x) также
возрастает. Док-ем что V’(х)=S(x). Док-во:
придадим х произвольное приращение ![]() , такое
чтобы
, такое
чтобы![]() , тогда проведём сечение и получим
приращение ф-ии
, тогда проведём сечение и получим
приращение ф-ии ![]() , где
, где ![]() -объём
заключённый м-ду плоскостями Qx и
-объём
заключённый м-ду плоскостями Qx и ![]() . Поскольку ф-ия S(x)
непрерывна на [a;b], то она будет также непрерывна на от-ке
. Поскольку ф-ия S(x)
непрерывна на [a;b], то она будет также непрерывна на от-ке ![]() , а следовательно по св-ву непрерывн. ф-ий
дастигает своего наименьшего и наибольшего значения (m,M).
Построим 2 прямые цилиндрического тела с основанием m и M и
высотой
, а следовательно по св-ву непрерывн. ф-ий
дастигает своего наименьшего и наибольшего значения (m,M).
Построим 2 прямые цилиндрического тела с основанием m и M и
высотой ![]() . Сравним величины
. Сравним величины ![]()
![]() - ограничена сверху целиндрич. телом с
основанием M, снизу-m. Разделим на
- ограничена сверху целиндрич. телом с
основанием M, снизу-m. Разделим на ![]() получим
получим
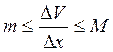 перейдём в данном нер-ве к lim при
перейдём в данном нер-ве к lim при
![]() .
. ![]() .
. 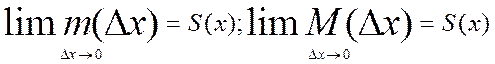
Т.о. по теореме о сжатой переменной т.к. ф-ия S(x) непрерывна, получим что
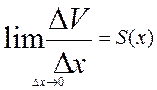
Что равносильно утверждению V’(х)=S(x). Следовательно V(х) является первообразной ф-ии S(x) на [a,b]
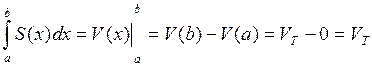 ч.т.д.
ч.т.д.
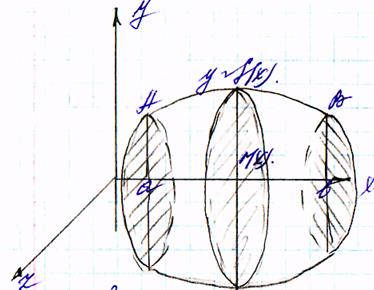
Объём тела вращения
Частным случаем задачи об V тела по S поперечных сечений, является задача об V тела вращения.
Пусть на плоскости Оху задана криволинейная трапеция ограничена непрерывной ф-ей f(x) прямыми х=а и х=b, и осью абсцисс. Тело вращения (Твр) образованное вращением криволинейной трапеции аАBb вокруг оси Ох, так что каждая её точка описывает окружность с центром на оси Ох в пл. перпендикулярной оси вращения называется телом вращения.
Пок-ем,
что тело вращения кубируемое и выражается формулой 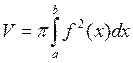
1. Тело вращения (Твр) заключённое между плоскостями х=а и х=b
2.
сечение Qx тело
вращения являются круги ![]() (r
определяет значение ф-ии f)
(r
определяет значение ф-ии f)
3. S(x) явл. непрерывной на от-ке [a;b] в силу того что ф-ия f непрерывна на этом от-ке по условию
4.
т.к. центры всех сечений Qx
лежат на оси Ох, то сечение Qx есть концентрические круги которые проектируются один
в другой поэтому применима формула 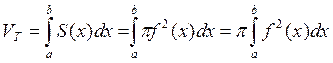 ч.т.д.
ч.т.д.
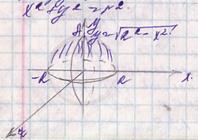
Н-р: вычислить V части шара, отсечённого плоскостью.
Будем рассматривать шар, тело вращения полученного от вращения круга.
![]()
-RAR вращение вокруг оси Ох
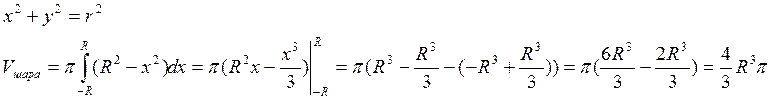
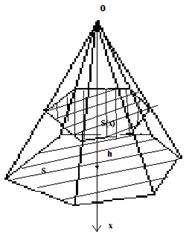
Вычисление V пирамиды высотой h и основанием S.
Возьмём с-му координат сначала в точке О, ось Ох пустим по высоте Оу и Оz перпендик. Ох. И воспользуемся фактором, т.к. S сечения пирамиды плоскостью перпендик. высоте относится как квадрат их расстояний от вершины пирамиды то имеем.
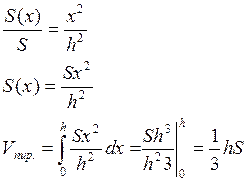
Вычисление V кругового конуса высотой h и радиуса основания R.
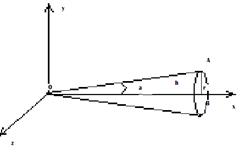
Выберем с-му корд. Oxyz, Ох совпало с высотой радиуса.
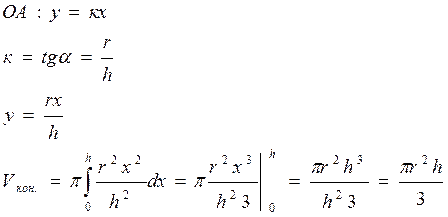
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.