Технологии сотрудничества реализуют демократизм, равенство, партнерство в субъект-субъектных отношениях педагога и ребенка. Учитель и учащиеся совместно вырабатывают цели, содержание, дают оценки, находясь в состоянии со-трудничества, со-творчества.
Технологии свободного воспитания делают акцент на предоставление ребенку свободы выбора и самостоятельности в большей или меньшей сфере его жизнедеятельности. Осуществляя выбор, ребенок наилучшим способом реализует позицию субъекта, идя к результату от внутреннего побуждения, а не от внешнего воздействия.)
Самые
сложные вопросы, связанные со скалярными величинами (длина,S, v, V,
время, угловая величина, температура, производительность, цена). В шк. курсе
понятие величины не даётся. Понятие величины можно ввести ч-з область её
определения. О1: Мн-во М называется областью определения
величины, если в ней определены 2 отношения: 1. бинарное (![]() ). 2. тернарное
). 2. тернарное ![]() и
выполняется следующие условия: а) сущ. хотя бы одно отображение f мн-ва
М во мн-во положительных действительных чисел
и
выполняется следующие условия: а) сущ. хотя бы одно отображение f мн-ва
М во мн-во положительных действительных чисел ![]() . (
. (![]() ), такое что эти эл-ты эквивалентны, тогда
образы равны (a эквивалентно b
), такое что эти эл-ты эквивалентны, тогда
образы равны (a эквивалентно b ![]() ) б) если же
другое отображение мн-ва
) б) если же
другое отображение мн-ва ![]() ,указанными 2-я св-ми,
то g(a)=kf(a). отображение
f
,указанными 2-я св-ми,
то g(a)=kf(a). отображение
f ![]() будет называться измерением величины
, а f(a)- значением величины для эл-та а при данном измерении,
или мера а. Если из a эквивалентно b
будет называться измерением величины
, а f(a)- значением величины для эл-та а при данном измерении,
или мера а. Если из a эквивалентно b![]() и
обратно
и
обратно ![]() а эквивалентно b
а эквивалентно b ![]() , такая величина
называется простой (длина, градусная мера угла). Если не выполняется условие
, такая величина
называется простой (длина, градусная мера угла). Если не выполняется условие ![]() а эквивалентно b, то такая
величина не является простой, тогда эти объекты а и b будут
равновеликими (S, V, цена, время (заданное на мн-ве)) О2: Величиной
заданной отношением
а эквивалентно b, то такая
величина не является простой, тогда эти объекты а и b будут
равновеликими (S, V, цена, время (заданное на мн-ве)) О2: Величиной
заданной отношением ![]() и
и ![]() на мн-ве
М, называется разбиение этого мн-ва М на классы эквивалентности по отношению «а
равновелико в » . Для каждой величины существует свои единицы измерения. Уже в
начальн. шк. ученики знают, что величины одного рода можно складывать и
умножать на число, других операций над ними нет. О: пусть М обл.
определённой величины с отношениями
на мн-ве
М, называется разбиение этого мн-ва М на классы эквивалентности по отношению «а
равновелико в » . Для каждой величины существует свои единицы измерения. Уже в
начальн. шк. ученики знают, что величины одного рода можно складывать и
умножать на число, других операций над ними нет. О: пусть М обл.
определённой величины с отношениями ![]() и
и ![]() , а М1 обл. определённой величины
со следующими отношениями
, а М1 обл. определённой величины
со следующими отношениями ![]() (усиленное),
(усиленное), ![]() и пусть
и пусть ![]() . Если
кроме того мн-во М1 явл. областью определения некоторой величины, то
соответств. величина оме того мн-во М ми ошениями й
над ними нет.ывать й определены 2 отношенияв М1 назыв.
распространением заданной величины из М в М1. в шк. курсе V
получает следующее распространение: 1. на мн-ве многогранников; 2. мн-во фигур
вращения. Самым трудным моментом в шк. курсе явл. определение некоторых
скалярных величин. Лучше задать определение V тела не на мн-ве
геометрических фигур, а на мн-ве геометрических тел. Т.к. геометрическое тело
обладает всеми св-ми простой пространственной фигуры. (V-ом называется не
отрицательная величина, заданная на мн-ве геометрических тел и обладающая
св-ми:
. Если
кроме того мн-во М1 явл. областью определения некоторой величины, то
соответств. величина оме того мн-во М ми ошениями й
над ними нет.ывать й определены 2 отношенияв М1 назыв.
распространением заданной величины из М в М1. в шк. курсе V
получает следующее распространение: 1. на мн-ве многогранников; 2. мн-во фигур
вращения. Самым трудным моментом в шк. курсе явл. определение некоторых
скалярных величин. Лучше задать определение V тела не на мн-ве
геометрических фигур, а на мн-ве геометрических тел. Т.к. геометрическое тело
обладает всеми св-ми простой пространственной фигуры. (V-ом называется не
отрицательная величина, заданная на мн-ве геометрических тел и обладающая
св-ми: ![]() ). Геометрическое тело – такая ограниченная и
замкнутая пространственная фигура, которая обладает следующими св-ми: 1. она
содержит внутренность такую, что любые 2 точки которой можно соединить линией,
которая состоит только из внутренних точек; 2. граница внутренности совпадает с
границей фигуры. Изучается в 11кл. рассматривают единицы измерения. Выводят
формулы, проходят: понятие V, V прямоугольного параллелепипеда, прямой призмы,
цилиндра, наклонной призмы, пирамиды, конуса, вычисление V тел с
помощью определённого интеграла, V шара, шарового сегмента, шарового слоя, шарового
сектора, S сферы. 2-а тела равны если их можно совместить
наложением. V прямоугольного параллелепипеда равен произвед. 3-х его
измерений, V прямоугольн. параллелепип. равен произвед S
основания на h, V прямой призмы(основание- прямоугольн.
треугольник)=произвед. S основания на h, V цилиндра
=произвед. S основания на h, V наклонной призмы
=произвед. S основания на h, V пирамиды = одной
третьи произвед. S основания на h,
). Геометрическое тело – такая ограниченная и
замкнутая пространственная фигура, которая обладает следующими св-ми: 1. она
содержит внутренность такую, что любые 2 точки которой можно соединить линией,
которая состоит только из внутренних точек; 2. граница внутренности совпадает с
границей фигуры. Изучается в 11кл. рассматривают единицы измерения. Выводят
формулы, проходят: понятие V, V прямоугольного параллелепипеда, прямой призмы,
цилиндра, наклонной призмы, пирамиды, конуса, вычисление V тел с
помощью определённого интеграла, V шара, шарового сегмента, шарового слоя, шарового
сектора, S сферы. 2-а тела равны если их можно совместить
наложением. V прямоугольного параллелепипеда равен произвед. 3-х его
измерений, V прямоугольн. параллелепип. равен произвед S
основания на h, V прямой призмы(основание- прямоугольн.
треугольник)=произвед. S основания на h, V цилиндра
=произвед. S основания на h, V наклонной призмы
=произвед. S основания на h, V пирамиды = одной
третьи произвед. S основания на h, 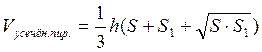 ,
, 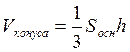 ,
, 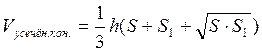 ,
,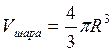 . Шаровой сегмент – часть шара,
отсекаемая от него какой-нибудь плоскостью.
. Шаровой сегмент – часть шара,
отсекаемая от него какой-нибудь плоскостью.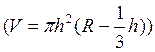 Шаровой
слой – часть шара, заключённая м-ду 2-я параллельными секущими плоскостями.
V = разности V 2-х шаровых сегментов. Шаровой сектор – тело,
полученное вращением кругового сектора с углом меньше 900 , вокруг
прямой , содержащей один из ограничивающих круговой сектор радиусов.
Шаровой
слой – часть шара, заключённая м-ду 2-я параллельными секущими плоскостями.
V = разности V 2-х шаровых сегментов. Шаровой сектор – тело,
полученное вращением кругового сектора с углом меньше 900 , вокруг
прямой , содержащей один из ограничивающих круговой сектор радиусов. 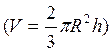
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.