При проведении научно-технических расчетов часто используются таблицы вида у(х), полученные экспериментальным путем. Неизбежно возникает задача получения сведений о поведении таких графических функций в промежутках между узловыми точками (интерполяция). Эта задача решается аппроксимацией исходной зависимости, т. е. ее подменой какой-либо достаточно простой функцией.
Структурная схема используемой нейронной сети для реализации задачи аппроксимации функции одной переменной.
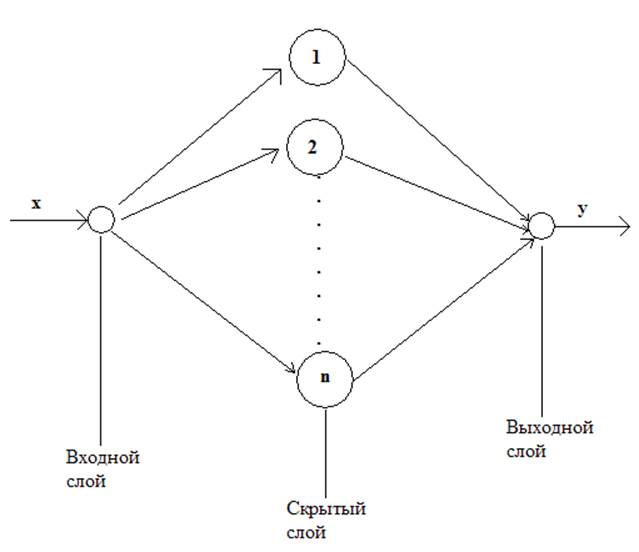
В нашем примере n=5;
Текст программы:
P=zeros(1,20); – создание массива
for i=1:20
P(i)=i*0.1; – входные данные (аргумент)
end
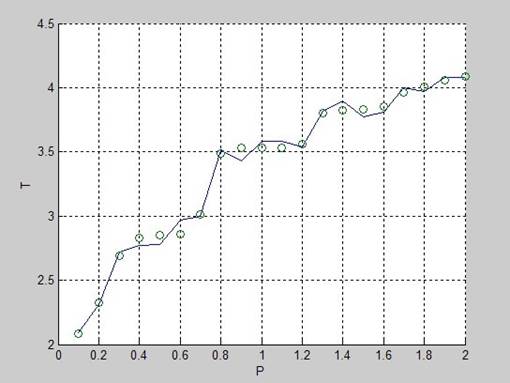
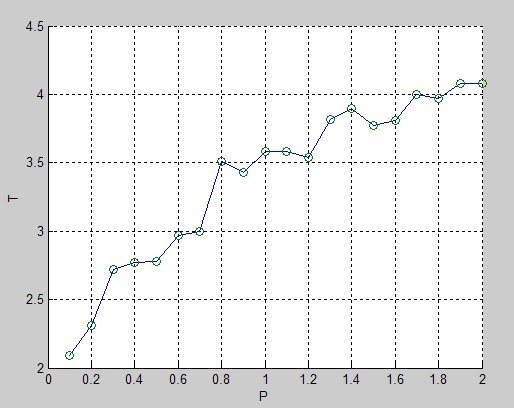
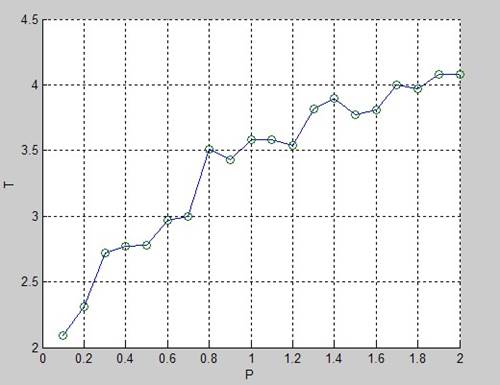
T=[2.09 2.31 2.72 2.77 2.78 2.97 3.00 3.51 3.43 3.58 3.58 3.54 3.82 3.90 3.77 3.81 4.00 3.97 4.08 4.08]
– входные данные (значение функции)
net=newff([0.1 2],[5 1],{'tansig' 'purelin'}); – создание нейронной сети
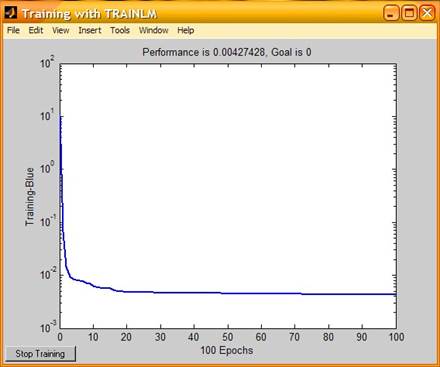
net.trainParam.epochs=100; – задание числа эпох обучения
net=train(net,P,T); – обучение сети
y=sim(net,P); – моделирование нейронной сети (net –имя сети, P- её выход)
figure (1);
hold on;
xlabel ('P');
ylabel ('T');
plot(P,T,P,y,'o'),grid; – прорисовка графика исходных данных и функции, сформированной нейронной сетью
Параметры нейронной сети
net=newff([0.1 2],[5 1],{'tansig' 'purelin'});
[0.1 2] – минимальное и максимальное значение x;
[5 1] – число Неронов в скрытом слое (5) и в выходном слое (1);
'tansig' – функция активации нейронов в скрытом слое (гиперболический тангенс);
'purelin' – линейная функция активации нейронов в выходном слое;
Изменения при построении графика при изменении числа нейронов в скрытом слое:
Число нейронов равно 5;
График
Эпохи обучения (100)
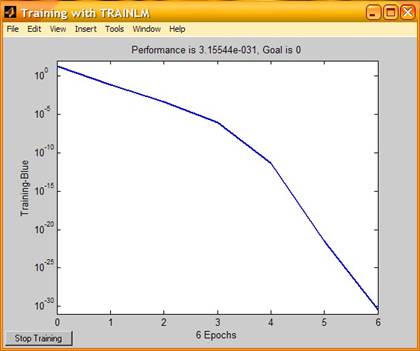
Число нейронов равно 20;
Эпохи обучения (6)
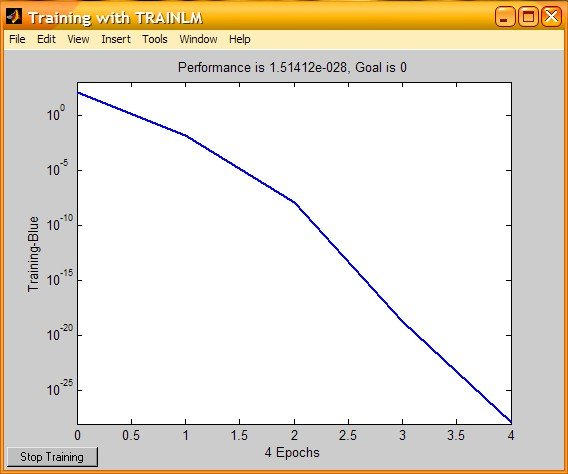
Число нейронов равно 1000;
Эпохи обучения (4);
Вывод:
В результате выполнения лабораторной работы я ознакомилась с основами теории искусственных нейронных сетей. В среде Matlab был создан программный код, с помощью которой была построена и обучена нейронная сеть с одним скрытым слоем без обратных связей для аппроксимации таблично заданной функции.
При увеличении числа нейронов в скрытом слое время решения задачи увеличивается, а число эпох обучения уменьшается. При небольшом числе нейронов в скрытом слое таблично заданная функция строиться методом приближения, при увеличении числа нейронов функция строиться методом интерполяции.
Я убедилась, что нейронные сети являются одним из мощных математических аппаратов для решения аппроксимации функций.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.