Если f(x)dx есть дифференциал функции F(X),to f(x)dx=dF(x). Функцию F(x) называют первообразной функции f(x). Наиболее общий вид первообразной функции f (х) называют неопределенным интегралом и обозначают следующим образом:
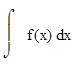
В состав этого выражения включена некоторая постоянная интегрирования С, подчеркивающая, что для одной и той же функции f(x) существует масса первообразных, описываемых одной и той же линией, но смещенных по вертикали на произвольную постоянную. О ее существовании надо помнить, хотя она of дельно в результате не показывается.
Символьные операции весьма привлекательны для получения аналитических выражений для сумм, произведений, производных, интегралов и т. д. Рисунок иллюстрирует применение символьных директив для вычисления интегралов. Здесь полезно обратить внимание на применение директивы float, позволяющей получить значение интеграла в виде обычного вещественного числа с заданным числом знаков мантиссы после десятичной точки.
4.2. Символьное вычисление пределов функций
Пределом функции f (х) называют то ее значение b, к которому функция неограниченно приближается в точке х=а (предел в точке) или слева либо справа от нее.
При этом подразумевается, что функция f(x) определена на некотором промежутке, включающем точку х=а и во всех точках, близких к ней слева и справа. В последнем случае предел вычисляется для х=а- h или х=а+h при h, стремящемся к нулю. Пределом может быть число, математическое выражение и положительная или отрицательная бесконечность. Последнее соответствует расширенному представлению о пределах.
Для вычисления пределов функций в MathCAD введена директива (оператор)limit. Помимо ввода с наборной панелиCalculusPallete ее можно ввести в трех различных формах нажатием следующих комбинаций клавиш:
Ø Ctrl+L — ввод шаблона директивы вычисления предела функции при х, стремящемся к заданному значению;
Ø Ctrl+A — ввод шаблона директивы вычисления предела функции слева от заданной точки;
Ø Ctrl+B — ввод шаблона директивы вычисления предела функции справа от выбранной точки.
На рисунке показаны примеры вычисления пределов трех функций. При вычислении пределов нужно заполнить места ввода шаблона для вычисления пределов, а затем ввести функцию, имя переменной, по которой ищется предел, и значение переменной (аргумента функции).
4.4. Символьные преобразования Фурье, Лапласа и Z-преобразование
Во многих прикладных задачах спектрального анализа и синтеза, в проектировании фильтров и в анализе сигналов важное значение имеют интегральные преобразования Фурье, Лапласа, а также Z- преобразования.
Реализация этих преобразований в среде MathCAD в символьном виде демонстрирует рисунок. Здесь показана цепочка: исходное выражение, затем прямое выражение и, наконец, обратное преобразование. В итоге должно получиться исходное выражение.
К сожалению, указанное правило соблюдается далеко не всегда. Если в результате прямого преобразования получается специальная функция (например Дирака), то последующее преобразование оказывается невозможным или не дает полного восстановления исходной функции. Такой случай представлен во втором примере на преобразование Фурье.
Для получения результата установите после блока вычисления предела символ —>. Предел (если он существует) будет вычислен, и результат появится в шаблоне около острия стрелки. Если функция не имеет предела, то вместо результата появится надпись Undefine.
4.3. Вычисление производных
Если f(x) — непрерывная функция аргумента х, то производная этой функции определяется следующим образом:
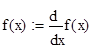 =
=
Таким образом, производная функции f(x) — это предел, к которому стремится отношение бесконечно малого приращения функции к соответствующему бесконечно малому приращению аргумента dx. Если речь идет о вычислении численного значения производной, то оно производится в некоторой точке х=х0. Как известно, значение производной геометрически характеризуется наклоном касательной к графику f(x) в точке х=0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.