Оператор символьного вывода. Директивы символьной математики, страница 2

Как видно на рисунках, решения с помощью операторов символьного вывода имеют следующие отличительные свойства:

Ø  дают хорошее визуальное представление операций;

Ø  имеют места ввода для задания параметров;

Ø  обеспечивают работу с функциями пользователя;

Ø  дают возможность передавать данные от формулы к формуле;

Ø  допускают расширение, позволяющее использовать сразу несколько директив;

Ø  имеют конструкцию, схожую с конструкцией программных блоков.

3.3. Решение систем уравнений, заданных в векторном виде

Весьма мощным средством символьной математики MathCAD 2000 является возможность решения систем нелинейных уравнений, заданных в векторной форме, с помощью директивы solve. Такая форма очень наглядна, о чем свидетельствует следующий рисунок, на котором показаны примеры решения с помощью директивы solve систем нелинейных уравнений, заданных в векторной форме.

Обратите внимание, что при таком задании исходных уравнений результат решения также представляется в векторной форме. Это значит, что он может быть целиком или частично использован в качестве входного выражения для дальнейших символьных вычислений.

4. Типовые примеры на символьные операции

Рассмотрим примеры на применение других представленных выше директив. На рисунке показано несколько примеров применения символьных вычислений. Здесь представлены директивыexpand (расширение выражений),solve (решение уравнений и неравенств) и substitute (подстановка). Полезно обратить внимание на то, что по отношению к исходному выражению можно применять операции неоднократно (особенно характерен последний пример) или применять различные операции (см. первый пример).

В этих примерах полезно обратить внимание на   множественность   применения  директив, особенно в примере на применение директивы подстановкиsubstitute. Примеры применения директивsimplify (упростить),series (разложить в ряд),lарlасе (выполнить преобразование Лапласа) иsolve приведены на рисунке:

Как нетрудно заметить, директива упрощенияsimplify не имеет параметров. Директива разложения в ряд Тейлораseries требует задания двух параметров — начального значения переменной x и количества членов ряда. Директивы преобразования ЛапласаLaplace (более подробно преобразование Лапласа будет рассмотрено ниже) и решения уравненийsolve требуют указания одного параметра — имени переменной (в нашем случае х). С помощью директивыsolveможно также решать системы уравнений — тогда в качестве параметра необходимо указать вектор неизвестных (примеры этого уравнения приводились выше).

Применение директивcomplex (комплексные вычисления),assume и coeffs (выделить коэффициенты полинома) поясняет рисунок.

Тут важно обратить внимание на двойственность применения ключевого слова assume. Оно может применяться для отмены значений переменных (берется прямо из палитры символьных директив) и для указания статуса и ограничений переменных (берется из дополнительной палитрыModifiers).

Выполнение матричных операций в символьной форме особой специфики не имеет. На рисунке показаны основные операции с матрицами, включая транспонирование матрицы, вычисление обратной матрицы и вычисление детерминанта матрицы. Для наглядности взята матрица небольшого (2х2) порядка.

4. Расширенные возможности символьных вычислений

4.1. Символьное вычисление интегралов

Если есть некоторая функция f(х), то показанный ниже определенный интеграл дает значение площади, ограниченной вертикалями а и b, именуемыми пределами интегрирования, кривой f(х) и осью абсцисс X:

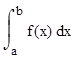
Такой интеграл обычно представляется числом (в общем случае комплексным), но может быть представлен и аналитическим выражением.