Аннотация.
Приведены дополнительные расчетные данные о скорости горения для типичных газовых смесей при давлениях до 6000 атм и температурах до 4000 К. Установлено, что основной вклад в скорость горения дает влияние начальной температуры, зависимость от давления весьма слабая. Для топливно-кислородных и топливно-воздушных смесей в трехмерном пространстве (давление-температура-скорость дефлаграционного горения) установлено существование единой поверхности скоростей горения и непрерывная зависимость скорости пламени от начальных условий.
Введение.
Одной из задач взрывоопасности горючих систем является моделирование реального сценария всех стадий развития взрыва: воспламенение смеси и формирование низкоскоростного ламинарного пламени, ускорение фронта пламени за счет естественной или искусственной турбулизации, формирование волн сжатия расширяющимся фронтом пламени, формирование слабой ударной волны (УВ) и ее последующее усиление, взрывное воспламенение сжатой смеси (за фронтом УВ перед фронтом пламени), взаимодействие этих нестационарных фронтов горения, приводящее при определенных условиях к возникновению детонационной волны (ДВ). Чаще всего ДВ возникает сначала в области сжатого и нагретого ударной волной газа, а затем ¾ после «догона» этой волной фронта головной УВ ¾ и к формированию ДВ в исходной смеси. Вышеописанная последовательность событий ¾ типичный сценарий перехода горения в детонацию (ПГД).
Нормальная скорость ламинарного горения определяется процессами диффузии и теплопроводности и для корректного их моделирования необходимо иметь информацию о зависимости этих коэффициентов от параметров среды, постоянно меняющихся в процессе ускорения пламени. Очевидно, что необходимы не только физически обоснованные модели турбулизации течения, но и корректные в широком диапазоне изменения основных газодинамических параметров зависимости всех основных коэффициентов, определяющих развитие процесса.
До сих пор традиционно зависимость скорости пламени W от давления P и температуры T задается в виде эмпирического соотношения (с большой степенью неопределенности)
![]() (1)
(1)
где индексом 00 отмечены значения параметров при некотором стандартном состоянии, а показатели n и m определяются на основе экспериментальных данных.
Подход.
К задаче о функциональной зависимости скорости горения W от давления и температуры (формула типа (1)) можно подойти с точки зрения задачи о распространении волн горения и детонации в реагирующих системах, основанной на законах сохранения массы, импульса и энергии (например, [1, 2]):
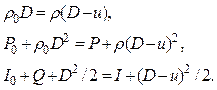 (2)
(2)
Здесь r ¾ плотность смеси (удельный объем ![]() ), P ¾ давление, D
и u ¾ волновая и массовая скорости, I ¾ энтальпия, Q ¾ энерговыделение смеси.
), P ¾ давление, D
и u ¾ волновая и массовая скорости, I ¾ энтальпия, Q ¾ энерговыделение смеси.
Для лучшего понимания изложим кратко основные моменты работы. В результате алгебраических преобразований из законов сохранения массы и импульса можно получить уравнение прямой Михельсона-Рэлея (ПМР), проходящей через точку начального состояния (P0, V0)
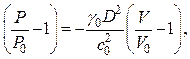 (2а)
(2а)
а из уравнения энергии (в
рамках модели идеального газа с независящей от температуры теплоёмкостью при
постоянном объеме![]() ) ¾
адиабату продуктов реакции P = f(V, Q) (адиабату энерговыделения (АЭ)):
) ¾
адиабату продуктов реакции P = f(V, Q) (адиабату энерговыделения (АЭ)):
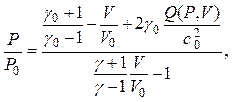 (2b)
(2b)
представляющую собой гиперболу в плоскости (P, V), выпуклую в сторону начала координат. Показатели адиабаты для исходной смеси и продуктов реакции обозначены как γ0и γ соответственно, энерговыделение Qсчитается постоянным на АЭ в рамках идеализированной одностадийной модели, или является переменной величиной вдоль АЭ (функцией параметров системы) в рамках модели химического равновесия продуктов. На рис. 1 схематически изображены ПМР 3 и 4, ударная адиабата 2 без энерговыделения, адиабата энерговыделения 1, а также все характерные точки. На этой АЭ выделяют детонационную (при P > P0 и V < V0) и дефлаграционную (при P < P0 и V > V0) ветви. Поскольку точка O исходного состояния лежит вне гиперболы, то из этой точки можно провести прямолинейные секущие (как к детонационной, так и к дефлаграционной ветвям адиабаты энерговыделения) с двумя точками пересечения этой прямой с каждой ветвью адиабаты энерговыделения. Точки пересечения стягиваются в одну, когда секущая превращается в касательную (самоподдерживающаяся волна Чепмена-Жуге). Замечательной особенностью системы уравнений для описания волн горения и детонации является то, что скорости волн, соответствующие условию касания ПМР 3 и 4 к детонационной и дефлаграционной ветвям, не являются произвольными, а оказываются взаимосвязанными. Это и позволяет решить поставленную задачу.
Рассмотрим
детонационную волну относительно точки исходного состояния О. Ударная волна переводит газ из состояния О в
состояние S,
соответствующее химпику ДВ, затем начинается химическая
реакция и после ее завершения продукты реакции попадают в точку D. Переход из S в D осуществляется
вдоль прямой Михельсона, являющейся касательной
к адиабате энерговыделения относительно исходного состояния О. Но прямая
Михельсона из О в S одновременно является касательной к адиабате
энерговыделения, проведенной из точки S как начальной [3]. Следует
уточнить, что адиабаты энерговыделения, построенные относительно точек О и S, не совпадают
друг с другом, сохраняется лишь условие и точка касания D. При этом
изэнтропа в точке D касается снизу адиабаты энерговыделения, построенной относительно точки О, и касается сверху
адиабаты, построенной относительно точки S. Иными словами,
точка D соответствует
как параметрам детонации относительно исходного состояния О, так и параметрам
дефлаграционного горения с исходным
состоянием в точке S. Отметим, что уже в классических работах (например, [1, 2])
высказывалась мысль о том, что детонация может быть представлена как горение за
ударной волной.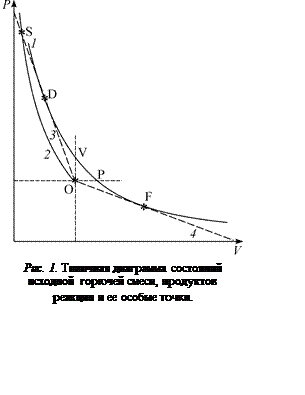
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.