Этот взгляд (со стороны детонации на горение) позволяет проанализировать изменение дефлаграционных скоростей в состояниях с различными начальными давлениями и температурами и даже получить аналитическую формулу для скорости дефлаграционного горения в зависимости от Р0 и Т0. В работе [4] состояние в химпике детонационной волны (ДВ) рассматривалось как исходное состояние для дефлаграционного горения в потоке горючей смеси за ударным фронтом ДВ в рамках модели идеального газа с постоянными Q и γ и была получена формула для оценки скорости горения в зависимости от исходных параметров смеси:
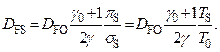 (3)
(3)
Последняя формула, кроме того, является обоснованием достаточно произвольной формулы (1).
Результаты и обсуждение.
Для проверки последнего соотношения были выполнены расчеты параметров горения и детонации стехиометрических смесей водорода и типичных углеводородов (метана, этилена и ацетилена, как представителей с одинарной, двойной и тройной химической связью) с кислородом и воздухом при варьировании начального давления в диапазоне 0,001-100 атм и начальной температуры ¾ в диапазоне 200-1800 K, заведомо перекрывающих области применения [5]. Результаты расчётов подтвердили справедливость предложенной формулы (3). Дополнительно были выполнены расчеты параметров горения и детонации при исходном состоянии, соответствующем точке S (одновременное изменение Р и Т). Следует подчеркнуть, что условие Q = const вдоль адиабаты энерговыделения является сильной идеализацией, оправданной только возможностью простых алгебраических преобразований с законами сохранения. Уже в приближении химического равновесия продуктов Q меняется вдоль адиабаты: например, для смеси 2Н2 + О2 в характерных точках адиабаты QD = 972,6, QV = 1057,5, QP = 1117,6, QDF = 1199,7 кал/г. Если в качестве начального выбрать состояние в точке S, то в точке D, представляющей дефлаграционную точку, QDF = 1580,4 кал/г. Сравнивая с величиной Q для точки D, как детонационной точки относительно состояния О, замечаем, что эти величины заметно различаются (см. вышеизложенное о несовпадении адиабат энерговыделения для точек О и S).
Следует отметить, что параметры точки S как исходного состояния не входят в начальную регулярную сетку давлений и температур {P0, T0}, поскольку ограничены рамками законов сохранения. Возникает естественный вопрос о том, укладываются ли скорости дефлаграционного горения для нерегулярных начальных условий на некую поверхность скоростей, построенных по сетке с регулярными данными. Другими словами, является ли поверхность скоростей горения единой для произвольных начальных дан-ных. На языке математики существование единой поверхности означает наличие непре-рывной зависимости решения от начальных условий. Использование точки S в качестве точки начального состояния расширяет диапазон температур до 4000 K, а диапазон давлений до 6000 атм.
Как отмечено выше, зависимость скорости горения DFO от начальных параметров {P0, T0} образуетповерхность скоростей горения в трехмерном пространстве {P0, T0, DFO}. Оказалось, что скорости горения DFS относительно состояния S с повышенными нерегулярными параметрами {PS, TS} также принадлежат поверхности {P0, T0, DFO} скоростей горения, образованной регулярной начальной сеткой {P0, T0}. Это иллюстрирует рис. 2, например, для смеси водорода с воздухом. На рисунках изображена общая поверхность для разных групп данных: {P0, T0, DFO}, и {PS, TS, DFS}. Это свидетельствует о существовании единой поверхности скоростей горения для различных режимов распространения. Другими словами ¾ наблюдается непрерывная зависимость решения (скорость пламени) от начальных условий.
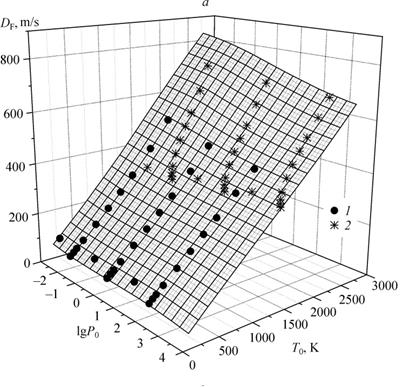
Рис. 2.Поверхность скоростей горения для смеси водорода с воздухом.
1 ¾ DFO, 2 ¾ DFS.
Заключение.
Таким образом, в настоящей работе приведены дополнительные расчетные данные о скорости горения для типичных газовых смесей при давлениях до 6000 атм и температурах до 4000 K. Установлено, что основной вклад в скорость горения дает влияние начальной температуры, зависимость от давления весьма слабая. Скорости горения DFO для топливно-кислородных и топливно-воздушных смесей в зависимости от начальных параметров {P0, T0} образуют единуюповерхность в трехмерном пространстве {P0, T0, DFO}, что свидетельствует о непрерывной зависимости решения (скорость пламени) от начальных условий.
Список литературы.
1. Митрофанов В.В. Детонация гомогенных и гетерогенных систем. Новосибирск: Изд-во Инст-та гидродинамики им. М. А. Лаврентьева СО РАН, 2003. 200 с.
2. Зельдович Я.Б., Компанеец А.С. Теория детонации. М.: Гостехиздат, 1955. 269 с.
3. Щелкин К.И., Трошин Я.К. Газодинамика горения. М.: Из-во Академии наук СССР, 1963. 256 с.
4. Васильев А.А. Оценка зависимости скорости пламени от давления и температуры // ФГВ. 2011. Т. 47, № 5. С. 13-17.
5. Васильев А.А. Экспериментальная оценка скорости горения взрывчатой смеси при повышенных давлениях и температурах // ФГВ. 1992. Т. 28, № 4. С. 44-48.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.