Рассмотрим радиальные колебания аксиально симметричного фронта пламени, при радиальном истечении топлива из центра.
1. Уравнения, описывающие установившиеся течения смеси и продуктов, являются уравнениями акустики – уже линейные:
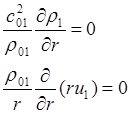 в обл. 1 – смесь
в обл. 1 – смесь
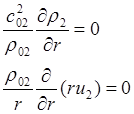 в обл. 2 – продукты
в обл. 2 – продукты
Получены линеаризацией уравнений газовой динамики на покой.
Решения: 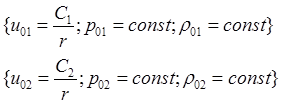
Граничные условия на стационарном радиусе горения (там и располагается фронт пламени):
![]()
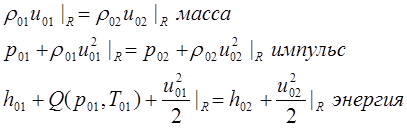
Для газов берётся модель идеальных газов с постоянными теплоёмкостями, тогда:
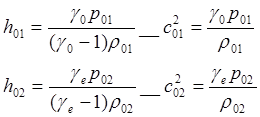
Разные показатели политропы перед и за скачком. Энерговыделение смеси можно рассчитать, зная данные о скорости горения в зависимости от давления и температуры. Это делается путём добавления к граничным условиям условия Чепмена-Жуге для расчёта скорости фронта (условия касания адиабаты энерговыделения (энергия) и прямой Михельсона (импульс)). Скорость горения должна быть направлена против скорости течения топлива и равна ей по модулю на стационарном радиусе горения - из этого условия и находится стационарный радиус горения.
2. Линеаризация задачи по малым амплитудам:
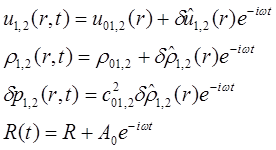 индексы
1 и 2 – областях «1» и «2», соответственно
индексы
1 и 2 – областях «1» и «2», соответственно
Уравнения линеаризовывать не надо!!
Уравнения (время уже отделили):
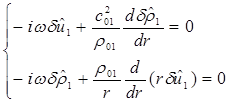 в
области «1» (1.1)
в
области «1» (1.1)
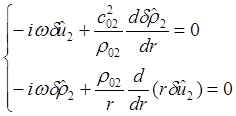 в
области «2» (1.2)
в
области «2» (1.2)
Из этих уравнений получаются уравнения Гельмгольца для областей 1 и 2 на возмущения плотностей:
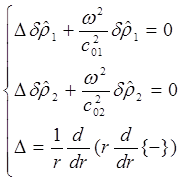 (1.3)
(1.3)
Для возмущения скоростей получаются такие же уравнения.
Граничные условия для возмущённой границы:
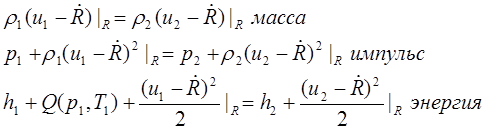
Линеаризованные граничные условия:
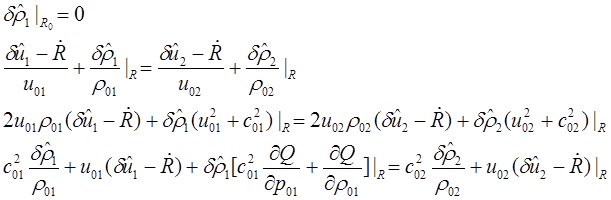 (1.4)
(1.4)
В линеаризованных граничных условиях, все значения функций сносятся на найденную среднюю линию – радиус стационарного горения.
3 . Анализ корректности задачи
Решение задачи для комплексных амплитуд будет выражаться через функции Ганкеля первого и второго рода:
![]()
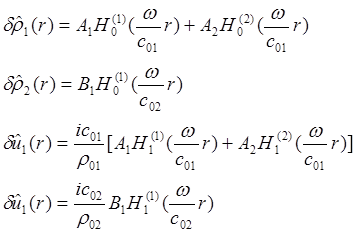
Для области 2 функция
Ганкеля второго рода в решениях отсутствует в силу условия излучения
Зоммерфельда. Без ограничения общности можно считать, что ![]() , тогда возмущение
плотности в области 1 будет действительным:
, тогда возмущение
плотности в области 1 будет действительным: ![]() . Между
возмущениями плотности и скорости через основные уравнения есть связь,
следующая из (1.1) и (1.2):
. Между
возмущениями плотности и скорости через основные уравнения есть связь,
следующая из (1.1) и (1.2):
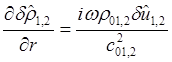 (1.5)
(1.5)
Пусть w -комплексная частота акустических возмущений с положительной мнимой частью (спектр – в верхней полуплоскости комплексной плоскости C).Тогда решение будет расти по времени и затухать по пространству в области 2 согласно асимптотическому поведению функции Ганкеля на бесконечности. Помножим уравнения (1.3) на комплексно сопряжённые функции и проинтегрируем по всей области колебаний:
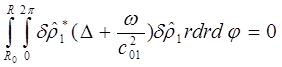 (a)
(a)
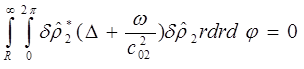 (b)
(b)
Сложим их:
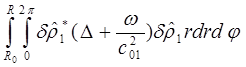 +
+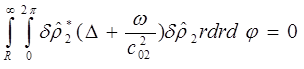 (c)
(c)
Преобразуем полученное выражение (c):
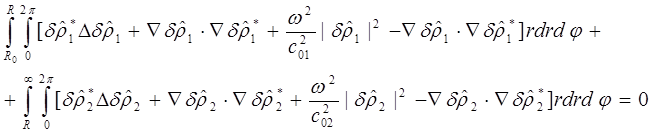
Преобразуем два первых слагаемых в подъинтегральных выражениях по теореме Грина в интегралы по границе, так как на границах у нас есть граничные условия:
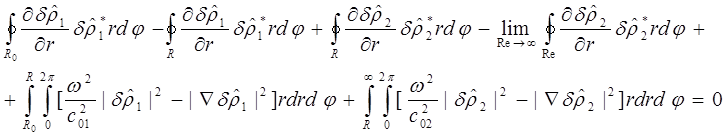
Первый интеграл по
границе в этом выражении будет равен нули в силу граничного условия на границе R0:
![]() , четвёртый интеграл по границе
будет равен нули при стремлении радиуса границы к бесконечности, согласно
асимптотическому поведению функций Ганкеля на бесконечности и выбранному положительному
знаку мнимой части частоты. Учтя всё это, таким образом, получим:
, четвёртый интеграл по границе
будет равен нули при стремлении радиуса границы к бесконечности, согласно
асимптотическому поведению функций Ганкеля на бесконечности и выбранному положительному
знаку мнимой части частоты. Учтя всё это, таким образом, получим:
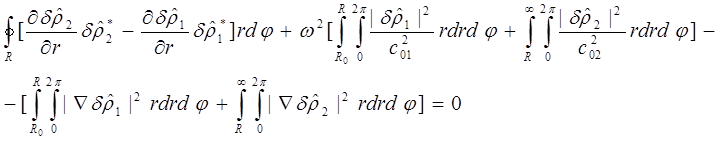 (d)
(d)
Рассмотрим подробнее
интеграл по границе в выражении (d).
Из граничных условий (1.4), исключая скорость колебания границы ![]() можно найти связь между возмущениями
плотности и скорости через линию скачка горения:
можно найти связь между возмущениями
плотности и скорости через линию скачка горения:
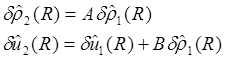 (e)
(e)
где A и B – действительные константы, зависящие от параметров стационарного решения на границе скачка. Производные возмущений плотности связаны соотношениями (1.5):
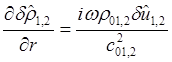
Итак:
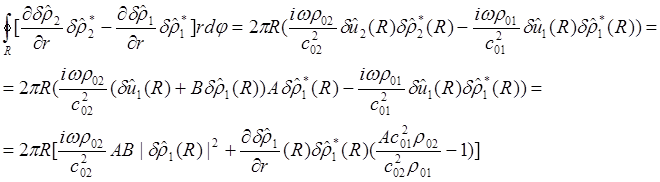
Второе слагаемое в
найденном выражении для интеграла по границе является действительным числом
,так как ![]() .
.
Возьмём теперь мнимую часть от выражения (d), учитывая найденное выражение для интеграла по границе:
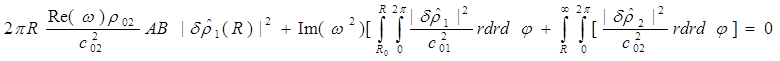 (f)
(f)
Последние интегралы в выражении (d) по области колебаний от квадратов модулей градиентов возмущений в мнимую часть выражения (f) не вошли, так как являются действительными числами.
Таким образом из выражения (f) видно, что существуют отличные от нуля акустические возмущения с собственными частотами с положительной мнимой частью. То есть аксиально симметричный фронт пламени неустойчив по малым радиальным возмущениям фронта
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.