3.1. МЕТОДЫ РАСЧЕТА И ОПТИМИЗАЦИИ ПАРАМЕТРОВ ДИРЕКТОРНЫХ АНТЕНН
Современное производство имеет тенденцию к сокращению сроков разработки изделий, повышению качеству разработки. Поэтому широкое применение находят системы автоматизированного проектирования (САПР) узлов, деталей, конструкции изделия. Все это относится и к разработке антенной технике. В основе любой САПР лежит ядро, которое на основе математической модели реализует физические принципы проектируемого изделия. Качество проектирования зависит насколько математическая модель адекватна физическим процессам, происходящим в реальном объекте. Антенна, в этом смысле, является сложным физическим объектом. В основе ее работы лежат не тривиальные процессы взаимодействия электро-магнитных полей.
Универсальные математические модели антенн строятся на основе решения системы уравнений Максвела для конкретной граничной задачи. Решение подобного типа граничных задач сопряжено с большими математическими и вычислительными трудностями. Поэтому применяют упрощенные математические модели. Например, для расчета апертурных антенн используют методы физической и геометрической оптики, а для расчета тонкопроволочных антенн – метод наводимых ЭДС и метод обобщенных наводимых ЭДС. Упрощенные методы дают качественную оценку работы антенн. Изготовление по этим данным антенн требует серьезной экспериментальной доработки, что увеличивает сроки проектирования изделия. Бурное развитие вычислительной техники, совершенствование математического аппарата делают возможным применение строгих электродинамических моделей в ядре САПР. Применительно к решаемой в данном дипломном проекте задаче, математическая модель исследуемой ШДА строится на основе аппарата интегральных уравнений (ИУ). В данном разделе показаны различные ИУ, полученные на основе уравнений Максвела, относительно неизвестной функции тока, по элементам антенны.
Распределение тока по антенне и поле, созданное этим током, должны удовлетворять уравнению Максвелла:
![]()
![]() , ( 1 )
, ( 1 )
где ![]() - вектор плотности
тока.
- вектор плотности
тока.
Вектор
напряженности электрического ![]() и магнитного
и магнитного ![]() полей могут быть выражены через
векторный потенциал
полей могут быть выражены через
векторный потенциал ![]() :
:
![]() ( 2 )
( 2 )
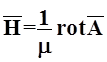 ,
,
где
![]()
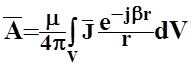 ,
,
где ![]() - расстояние от
точки интегрирования с координатами
- расстояние от
точки интегрирования с координатами ![]() до точки
наблюдения с координатами
до точки
наблюдения с координатами ![]() ;
; ![]() - коэффициент фазы;
- коэффициент фазы; ![]() - объем, включающий в себя все
области , в которых имеются точки.
- объем, включающий в себя все
области , в которых имеются точки.
При решении задачи о распределении токов необходимо учесть граничные условия на поверхности антенны. В такой постановке задача нахождения распределения тока по антенне сводится к решению некоторого интегрального уравнения.
Раздел о тонкопроволочных антеннах в теории антенн занимает очень важное положение. Ряд стандартных предположений и подходов, описываемых ниже, впервые развитых в применении к тонкопроволочным антеннам широко используется в практике инженерных расчетов многих антенн более сложных типов.
Рассмотрим
случай произвольно изогнутого тонкого излучателя длиной ![]() с
круглым поперечным сечением радиуса
с
круглым поперечным сечением радиуса ![]() , помещенного в
однородную изотропную среду без потерь.
, помещенного в
однородную изотропную среду без потерь.
Разместим
излучатель в криволинейной системе координат, в которой координата ![]() отсчитывается вдоль оси изогнутого
излучателя, совпадающего с осью криволинейной системы координат ( рис. 2 ).
Поперечное сечение излучателя, в котором отсчитывается угол
отсчитывается вдоль оси изогнутого
излучателя, совпадающего с осью криволинейной системы координат ( рис. 2 ).
Поперечное сечение излучателя, в котором отсчитывается угол ![]() , перпендикулярно его оси,
, перпендикулярно его оси, ![]() ,
, ![]() и
и
![]() - единичные векторы, касательные к оси
излучателя в сечениях
- единичные векторы, касательные к оси
излучателя в сечениях ![]() и
и ![]() .
.
Под
действием стороннего электрического поля ![]() на
поверхности проводника возникнут электрические токи. Напряженность электрического
поля, созданная этими токами, в том числе на поверхности проводника,
определяется известной формулой:
на
поверхности проводника возникнут электрические токи. Напряженность электрического
поля, созданная этими токами, в том числе на поверхности проводника,
определяется известной формулой:
![]()
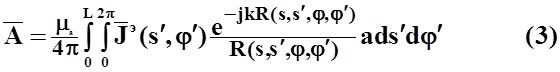
![]()
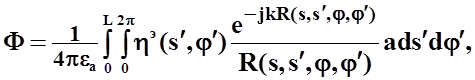
где ![]() - скалярный
потенциал.
- скалярный
потенциал.
![]() - поверхностные плотности тока и
заряда,
- поверхностные плотности тока и
заряда, ![]() - расстояние между точкой наблюдения
и точкой интегрирования.
- расстояние между точкой наблюдения
и точкой интегрирования.
Интегрирование
в формулах ![]()
проводится по поверхности цилиндрического излучателя, точка наблюдения также находится на его поверхности.
Известно, что для достаточно тонкого проводника, когда
![]()
поперечной составляющей плотности тока, зависимостью
от координаты ![]() продольной составляющей, а
также торцевыми токами можно пренебречь. Аналогичные замечания относятся и к
плотности заряда. Таким образом, получим:
продольной составляющей, а
также торцевыми токами можно пренебречь. Аналогичные замечания относятся и к
плотности заряда. Таким образом, получим:
![]()
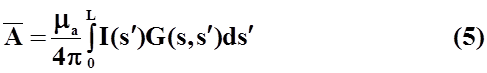
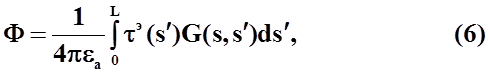
где ![]() -
ток излучателя;
-
ток излучателя;
![]() -
линейная плотность заряда;
-
линейная плотность заряда;
![]() -
функция Грина:
-
функция Грина:
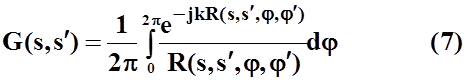
Дальнейшее
приближение, обычно используемое для тонких цилиндрических излучателей, состоит
в том, что в выражении для функции Грина ![]() принимается:
принимается:
![]()
где ![]() - расстояние
между точкой интегрирования
- расстояние
между точкой интегрирования ![]() , находящейся на
оси излучателя и точкой наблюдения
, находящейся на
оси излучателя и точкой наблюдения ![]() , находящейся на
его поверхности.
, находящейся на
его поверхности.
В этом случае:
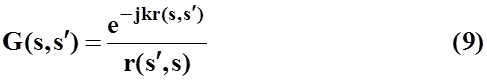
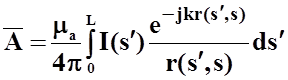
![]()
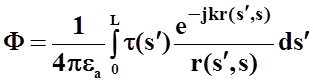
В случае гармонических токов и зарядов, линейная плотность заряда удовлетворяет уравнению непрерывности:
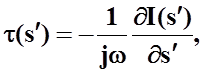
следовательно
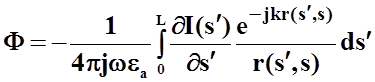
![]()
В выражениях ![]() ,
, ![]() интегрирование проводится по оси
проводника. Относительная ошибка, возникающая в связи с использованием
выражений
интегрирование проводится по оси
проводника. Относительная ошибка, возникающая в связи с использованием
выражений ![]() -
-![]() при
расчете поля на поверхности проводника, имеет порядок
при
расчете поля на поверхности проводника, имеет порядок 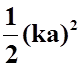 .
Для большинства практических случаев такой ошибкой можно пренебречь.
.
Для большинства практических случаев такой ошибкой можно пренебречь.
Будем считать проводник идеально проводящим. Тогда вектор созданный токами, протекающими по проводнику, должен удовлетворять условию
![]() .
. ![]()
Подставив
![]() ,
, ![]() в
в
![]() и приняв во внимание
и приняв во внимание ![]() ,получим:
,получим:
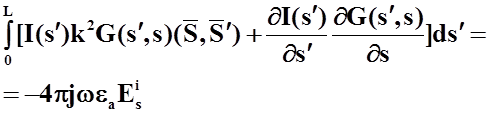
![]()
В
полученном выражении функция ![]() - известна.
Недостатком полученного уравнения
- известна.
Недостатком полученного уравнения ![]() является то, что
помимо функции тока в него в явном виде входит и производная функции тока. Это
обстоятельство вызывает определенные вычислительные трудности, однако проведя
ряд преобразований не трудно получить уравнение, в котором производная
исключена.
является то, что
помимо функции тока в него в явном виде входит и производная функции тока. Это
обстоятельство вызывает определенные вычислительные трудности, однако проведя
ряд преобразований не трудно получить уравнение, в котором производная
исключена.
Проинтегрировав
по частям второе слагаемое в ![]() , получим следующее
соотношение:
, получим следующее
соотношение:
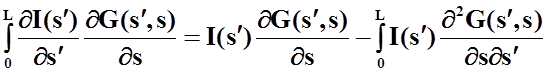 .
.
Интегрирование по частям производится следующим образом: если
![]() и
и ![]() имеют
в некотором интервале I непрерывные
производные, то
имеют
в некотором интервале I непрерывные
производные, то
![]() .
.
Первое
слагаемое в правой части полученного выражения равно нулю, так как
электрический ток на концах излучателя равен нулю. Таким образом, выражение ![]() преобразуется к виду:
преобразуется к виду:
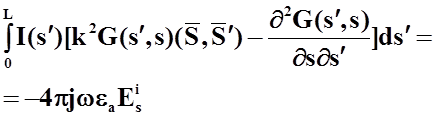 . (14)
. (14)
Полученное выражение представляет собой наиболее известный вид интегрального уравнения Поклингтона для произвольно изогнутого тонкопроволочного излучателя.
При
анализе тонкопроволочных структур широко используется интегральное уравнение
Мея. Наиболее просто оно может быть получено на основе преобразования
интегрального уравнения Поклингтона. С этой целью умножим обе части уравнения (14) на функцию 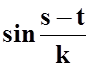 и
проинтегрируем полученное равенство по s в пределах от нуля до s . Подробно процесс получения
интегральных уравнений Мея из интегральных уравнений Поклингтона изложен в [5] . Приведем конечный результат:
и
проинтегрируем полученное равенство по s в пределах от нуля до s . Подробно процесс получения
интегральных уравнений Мея из интегральных уравнений Поклингтона изложен в [5] . Приведем конечный результат:
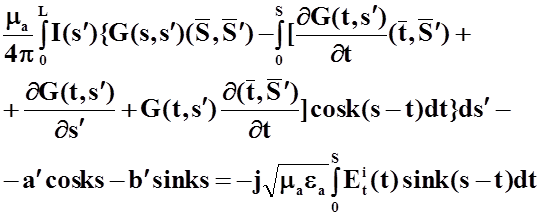 (15)
(15)
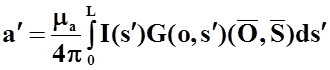 (16)
(16)
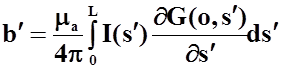 (17)
(17)
Уравнение (15) в иной форме было получено в работе Мея.
В частном случае прямолинейного цилиндрического проводника, возбуждаемого в центре дельтообразным источником (рис. 3), интегральное уравнение (15) преобразуется в хорошо известное интегральное уравнение Галлена.
Действительно, излучатель на рис. 3 состоит из двух элементов, у которых токи на симметричных точках равны по величине и одинаково направлены. В этом случае, когда точка наблюдения находится на верхнем провод
нике, имеют место следующие соотношения.
Поскольку
![]() , где
, где ![]() -
напряжение источника наблюдения,
-
напряжение источника наблюдения, ![]() - дельта-функция
Дирака.
- дельта-функция
Дирака.
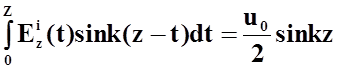 (18)
(18)
Функции Грина при интегрировании по верхнему проводнику имеет вид:
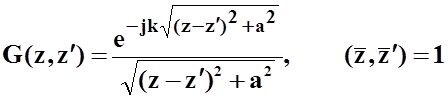 .
.
При интегрировании по нижнему проводнику:
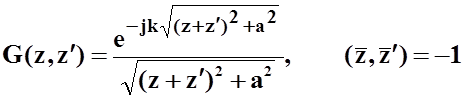 .
.
Таким
образом 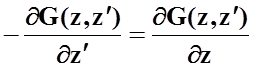 . Следовательно,
. Следовательно, ![]() , а уравнение (15) принимает вид:
, а уравнение (15) принимает вид:
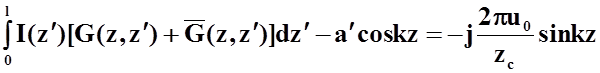 .
.
Для
интегрирования в пределах –l до l , то есть когда переменная ![]() принимает и
отрицательное значение, интегральное уравнение Галена может быть записано в
следующем виде:
принимает и
отрицательное значение, интегральное уравнение Галена может быть записано в
следующем виде:
![]()
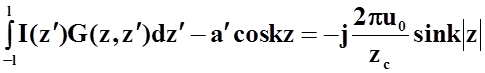 (19)
(19)
Такой вид интегрального уравнения Галена встречается наиболее часто.
Формально
на основании любого из полученных интегральных уравнений: Поклингтона - (14) , Мея - (15) , Галлена - (19) можно найти функцию распределения
тока ![]() , а затем вычислить все интересующие
нас электродинамические характеристики излучателя, такие, например, как
диаграмма направленности (ДН) излучателя, его входное сопротивление,
коэффициент усиления, коэффициент отражения (
, а затем вычислить все интересующие
нас электродинамические характеристики излучателя, такие, например, как
диаграмма направленности (ДН) излучателя, его входное сопротивление,
коэффициент усиления, коэффициент отражения ( ![]() ),
коэффициент стоячей волны (КСВ) и другие параметры излучателя. Однако эффективность
решения данной задачи для конкретной антенны в значительной степени
определяется выбором вида интегрального уравнения. Такой выбор для каждого
конкретного случая можно сделать, рассмотрев методы решения интегральных
уравнений и сопоставив преимущество и недостатки того или иного уравнения.
Подробно преимущества и недостатки разного вида интегральных уравнений
рассмотрены в разделе 3.3 «Численный алгоритм решения системы интегральных
уравнений Галленовского типа».
),
коэффициент стоячей волны (КСВ) и другие параметры излучателя. Однако эффективность
решения данной задачи для конкретной антенны в значительной степени
определяется выбором вида интегрального уравнения. Такой выбор для каждого
конкретного случая можно сделать, рассмотрев методы решения интегральных
уравнений и сопоставив преимущество и недостатки того или иного уравнения.
Подробно преимущества и недостатки разного вида интегральных уравнений
рассмотрены в разделе 3.3 «Численный алгоритм решения системы интегральных
уравнений Галленовского типа».
![]()
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.