Экономико-математические модели экономических систем. Практикум по курсу

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Ивановская государственная текстильная академия»

Кафедра бухгалтерского учета и аудита

Практикум по курсу

«Экономико-математические модели экономических систем»

для студентов специальностей 080502 (060800)

«Экономика и управление на предприятии (по отраслям)»,

080109 (060500) «Бухгалтерский учет и аудит»

Иваново 2005

В методических указаниях изложены теоретические основы экономико-математических методов по основным разделам этого курса, подробно разобраны примеры решения типовых задач и приведены задания для работы студентов на практических занятиях и для самостоятельной домашней работы.

Практикум по курсу «Экономико-математические модели экономических систем» предназначен для студентов специальности 080502 (060800) «Экономика и управление на предприятии (по отраслям)», 080109 (060500) «Бухгалтерский учет и аудит» дневной и заочной формы обучения.

Составитель 

Научный редактор

Редактор

Корректор

__________________________________________________________________

Лицензия ИД №06309 от 19.11.2001. Подписано в печать

Формат 1/16 60´84. Бумага писчая. Плоская печать. Усл. печ. л.

Редакционно – издательский отдел

Ивановской государственной текстильной академии

Участок оперативной полиграфии

153000 г. Иваново, пр. Ф.Энгельса, 21

Тема № 1.

Построение экономико-математических моделей задач оптимального

годового производственного планирования

В общем виде задача оптимального годового производственного планирования по критерию максимизации прибыли имеет следующий вид:

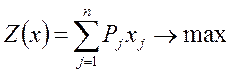
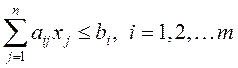
 - прибыль от реализации единицы продукции вида j,

 - объем производства продукции вида j,

 - норма затрат ресурсов вида  на производство единицы продукции вида ,

 - заданные объемы ресурсов вида .

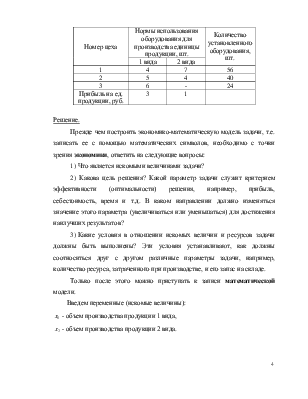
Пример 1.1. На предприятии производится два вида продукции на оборудовании, установленном в трех цехах. Известны нормы использования оборудования для производства единицы продукции в каждом цехе, количество установленного оборудования в каждом цехе, прибыль от производства единицы продукции каждого вида. Построить экономико-математическую модель задачи для определения оптимального плана производства продукции по критерию максимизации прибыли. Данные задачи сведены в таблицу:

Решение.

Прежде чем построить экономико-математическую модель задачи, т.е. записать ее с помощью математических символов, необходимо с точки зрения экономики, ответить на следующие вопросы:

1) Что является искомыми величинами задачи?

2)  Какова цель решения? Какой параметр задачи служит критерием эффективности (оптимальности) решения, например, прибыль, себестоимость, время и т.д. В каком направлении должно изменяться значение этого параметра (увеличиваться или уменьшаться) для достижения наилучших результатов?

3) Какие условия в отношении искомых величин и ресурсов задачи должны быть выполнены? Эти условия устанавливают, как должны соотноситься друг с другом различные параметры задачи, например, количество ресурса, затраченного при производстве, и его запас на складе.

Только после этого можно приступать к записи математической модели.

Введем переменные (искомые величины):

 - объем производства продукции 1 вида,

 - объем производства продукции 2 вида.

Тогда прибыль от производства всей продукции 1^го вида составляет , а прибыль от производства всей продукции 2^го вида - . Суммируя прибыль от производства продукции 1^го и 2^го видов, получаем прибыль от производства всей продукции: .

Так как по условию задачи требуется максимизировать прибыль, то целевая функция запишется следующим образом:

.

Сформируем ограничения по количеству установленного оборудования в каждом цехе.  - количество оборудования, которое используется в первом цехе для производства 1^го вида продукции,  - количество оборудования, которое используется в первом цехе для производства 2^го вида продукции. Тогда  - количество оборудования, которое используется для производства продукции в первом цехе.

Так как в первом цехе установлено 56 единиц оборудования, то для производства продукции обоих видов в первом цехе не может использоваться больше, чем 56 единиц оборудования. Тогда можно записать следующее ограничение:

.

Рассуждая аналогично, получаем ограничения для второго и третьего