Задачи по теории графов. Основные понятия и решения задач, страница 4

= 5*D2 + D3 + 9*D4 + 2*D5 + 3*D6 + 4*D7 + 3*D8.

Ограничения

= D2 + D3 + D4,         ,   (т. А )

= D4 + D7 + D8,         ,   (т. D)

= D2 – D5 – D6,          ,   (т. В)

= D3 + D6 – D8,          ,   (т. Е)

= D5 – D7,                  .          (т. С)

Ответ: А→Е→D; min Z(X) = 4.

Целевая функция

= 5*E2 + E3 + 9*E4 + 2*E5 + 3*E6 + 4*E7 + 3*E8.

Ограничения

= E2 + E3 + E4,           ,   (т. А)

= E3 + E6 +E8,            ,   (т. Е)

= E5 - E7,                    ,          (т. С)

= E4 + E7 – E8,           ,   (т. D)

= E2 – E6 – E5,           .   (т. B)

Ответ: А→Е; min Z(X) = 1.

Целевая функция

= 5*F2 + F3 + 9*F4 + 2*F5 + 3*F6 + 4*F7 + 3*F8.

Ограничения

= F2 + F5 + F6,           ,   (т. B)

= F5 + F7,                   ,          (т. C)

= F2 – F4 – F3,            ,   (т. А)

= F3 + F6 – F8,            ,   (т. E)

= F4 + F8 – F7,            .   (т. D)

Ответ: В→C; min Z(X) = 2.

Целевая функция

= 5*G2 + G3 + 9*G4 + 2*G5 + 3*G6 + 4*G7 + 3*G8.

Ограничения

= G2 + G5 + G6,         ,   (т. B)

= G4 + G7 +G8,          ,   (т. D)

= G2 – G3 – G4,          ,   (т. А)

= G5 - G7,                   ,          (т. C)

= G3 + G6 – G8,          .   (т. E)

Ответ: B→C→D (или B→E→D); min Z(X) = 6.

Целевая функция

= 5*H2 + H3 + 9*H4 + 2*H5 + 3*H6 + 4*H7 + 3*H8.

Ограничения

= H2 + H5 + H6,         ,   (т. B)

= H3 + H6 +H8,          ,   (т. E)

= H2 – H3 – H4,         ,   (т. А)

= H5 - H7,                  ,          (т. C)

= H4 + H7 – H8,         .   (т. D)

Ответ: B→E; min Z(X) = 3.

Целевая функция

= 5*I2 + I3 + 9*I4 + 2*I5 + 3*I6 + 4*I7 + 3*I8.

Ограничения

= I5 + I7,                     ,           (т. C)

= I4 + I7 +I8,               ,   (т. D)

= I5 – I6 – I2,              ,   (т. B)

= I2 – I3 – I4,              ,   (т. А)

= I3 + I6 – I8,              .   (т. E)

Ответ: C→D; min Z(X) = 4.

Целевая функция

= 5*J2 + J3 + 9*J4 + 2*J5 + 3*J6 + 4*J7 + 3*J8.

Ограничения

= J5 + J7,                     ,           (т. C)

= J3 + J6 +J8,              ,   (т. E)

= J5 – J6 – J2,              ,   (т. B)

= J7 + J4 - J8,              ,   (т. D)

= J2 – J4 – J3,              .   (т. А)

Ответ: C→B→E; min Z(X) = 5.

Целевая функция

= 5*K2 + K3 + 9*K4 + 2*K5 + 3*K6 + 4*K7 + 3*K8.

Ограничения

= K4 + K7 +K8,          ,   (т. D)

= K3 + K6 + K8,         ,   (т. E)

= K7 – K5,                  ,          (т. C)

= K4 + K2 – K3,          .   (т. А)

= K5 – K6 – K2,          ,   (т. B)

Ответ: D→E; min Z(X) = 3.

Результаты расчетов представлены ниже

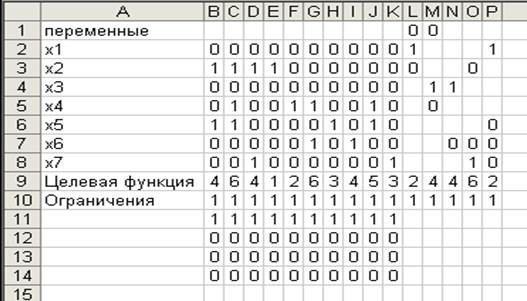
Рис. 3

Решение задачи 2 на ЭВМ

Для решения этой задачи достаточно прибавить к предыдущему решению кратчайший путь между вершинами АА, ВВ, СС, DD, EE следующим образом.

Вводим в ячейку L9 целевую функцию = 2*(5*L2 + L3+ 9*L4), которая соответствует уравнению . Вводим в ячейку L10 формулу = L2 + L3+ L4, что соответствует х₁ + х₂ + х₃ = 1.

Ответ: А→Е→А; min Z(X) = 2.

Аналогично находим d(B,B), d(C,C), d(D,D), d(E,E).

Целевая функция = 2*(5*М2 + 2*М5 + 3*М6).

Ограничение = М2 + М5+ М6,  х₁ + х₄ + х₅ = 1.

Ответ: В→С→В; min Z(X) = 4.

Целевая функция = 2*(2*N5 + 4*N7).

Ограничение = N5+ N7,  х₄ + х₆= 1.

Ответ: С→ В →C; min Z(X) = 4.

Целевая функция = 2*(9*O4 + 4*O7 + 3*O8).

Ограничение = O4 + O7+ O8,  х₃ + х₆ + х₇ = 1.

Ответ: D→E→D; min Z(X) = 6.

Целевая функция = 2*(P3 + 3*P6 + 3*P8).

Ограничение = P3 + P6+ P8,  х₂ + х₅ + х₇ = 1.

Ответ: E→A→E; min Z(X) = 2.

Результат представлен на рис. 3.

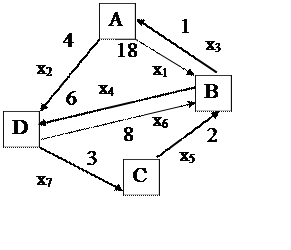
Решение задачи 3 на ЭВМ

Находим кратчайший путь между А и В.

1.Каждому ребру графа сопоставляем булевую (альтернативную) переменную х_i, , значение которой равно 1, если ребро входит в кратчайший путь, и равно 0 в противном случае.

2.Отводим под булевые переменные ячейки В2:В8.

3.Вводим в ячейку В9 целевую функцию

= 18*В2 + 4*В3 + В4 + 6*В5 + 2*В6 + 8*В7 + 3*В8, которой соответствует уравнение

.

4.Вводим в ячейки В10:В14 формулы соответствующих уравнений

= В2 + В3 - В4,                   ,                 (т. А)