Задачи по теории графов. Основные понятия и решения задач, страница 2

Символ "∞" означает, что связь не существует.

Над диагональю запишем длины кратчайших путей не более чем из одного ребра (в противном случае ∞).

Например, , d (D,А) = ∞,  .

Под диагональю запишем длины кратчайших путей не более чем из двух ребер (в противном случае ∞).

2). Построим табл. (Т₃).

Над диагональю запишем длины кратчайших путей не более чем из трех ребер (в противном случае ∞).

Например, d₁ (B,C) = d₁ (B, A)+d₁ (A, D) + d₁ (D, C) =++ = ,

d₂ (B, C) = d₂ (B, D) + d₂ (D, C) = +  =;

d (B, C) = min {d₁ (B, C); d₂ (B, C)} = min { ;} =  .

Таким образом, в табл. Т₃ записаны кратчайшие пути между вершинами данного графа.

Задача 4.Найти кратчайшие пути между всеми вершинами графа (см.рис. 2) через транзитные вершины.

1).Построим табл. (Т_*,А).

Запишем в клетки диагонали метки вершин A, B, C, D. Для них

d (A, A) = d (B, B) = d (C, C) = d (D, D) = d (E, E) = ∞.

Над диагональю запишем длины кратчайших путей не более чем из одного ребра (в противном случае  ∞).

Например,, , d (B, C) = ∞ .

Под диагональю запишем длины кратчайших путей не более чем из двух ребер через транзитную вершину А.

Например, длина пути BD через вершину А равна

d₁ (B, D) = d (В, А) + d (А, D) = +=;

d₂ (B, D) =, d (B, D) = min {;} =;

d (B, B) = d (B, A) + d (A, B) = + =. d (A, C) = ∞.

2) Построим табл. (Т_{в, с} ).

таблица (Т_*,А)                               таблица (Т_{в, с} )

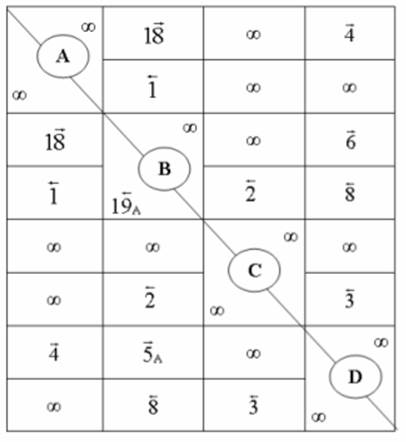
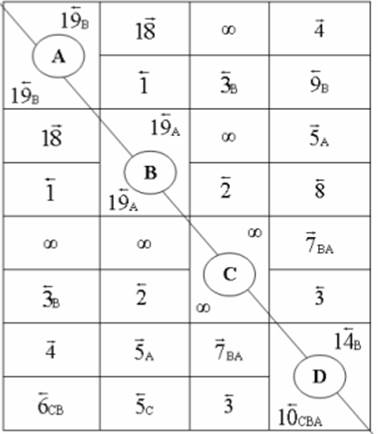
                                               таблица(Т_D)

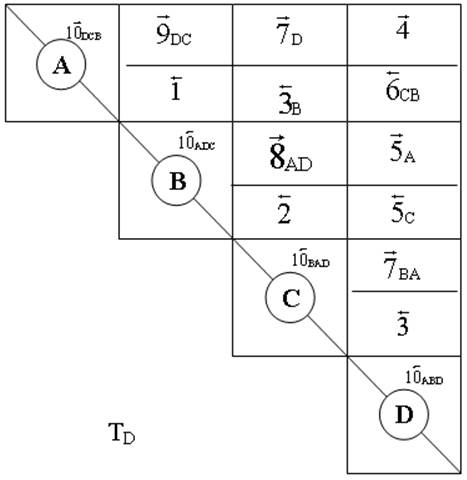
Над диагональю запишем длины кратчайших путей не более чем из трех ребер через транзитную вершину В (через А, или В, или АВ).

Например, d (С, A) =d (С, B) + d (B, A) = =  + =;

d₁ (С, D) = d₁ (С, В) + d₁ (В, D) =  +  =;

d₂ (С, D) = d₂ (С, В) + d₂ (В, A) +d₂ (A, D) =  +  + =;

d (C, D) = min{d₁ (C, D); d2 (C, D)} = min {;} =;

d (A, A) =d (A, B) + d (B, A) =  +  =;

d (D, D) =d (D, B) + d (B, D) = +  =;

d₁ (A, D) =, d₂ (A, D) = d₂ (A, B) + d₂ (B, D) =  +  =;

d (A, D) = min {;} =.

Под диагональю запишем длины кратчайших путей не более чем из четырех ребер через транзитную вершину С (через А, или В, или С, или АВ, или СВ, или ВА и т.д.).

Например, d₁ (D, A) = d₁ (D, B) + d₁ (B, A) =  +  =;

d₂ (D, A) = d₂ (D, C) + d₂(C, B) + d₂ (B, A) =  +  +  =;

d (D, A) = min {,} =;

d₁ (D, D) = d₁ (D, B) + d₁ (B, D) =  +  =;

d₂ (D, D) = d₂ (D, C) + d₂ (C, B) + d₂ (B, D) =  +  +  =;

d₃  (D,  D) = d₃  (D, С) + d₃  (C, B) + d₃  (B, A) + d₃  (A, D) = +  +  +  =;

d (D, D) = min {;;} = .

3).Построим табл.Т_D.

В каждую клетку запишем длину кратчайшего пути, не более чем из пяти ребер (через А, или В, или С, или В, или АВ, или ВА, или АД, или ДС и т.д.). Например,

d₁ (A, A) = d₁ (A, B) + d₁ (B, A) = =  +  =;

d₂ (A, A) = d₂ (A, D) + d₂ (D, B) + d₂ (B, A) = +  +  =;

d_{3 (}A, A) = d_{3 (}A, D) + d_{3 (}D, C) + d_{3 (}C, B) + d_{3 (}B, A) =  +   +  +  =;

d (A, A) =min {;;} =;

Таким образом, в табл. Т_D записаны кратчайшие пути между всеми вершинами данного графа через транзитные вершины.

Задача 5.   Построить минимальное дерево (рис. 3).

таблицу Т_*

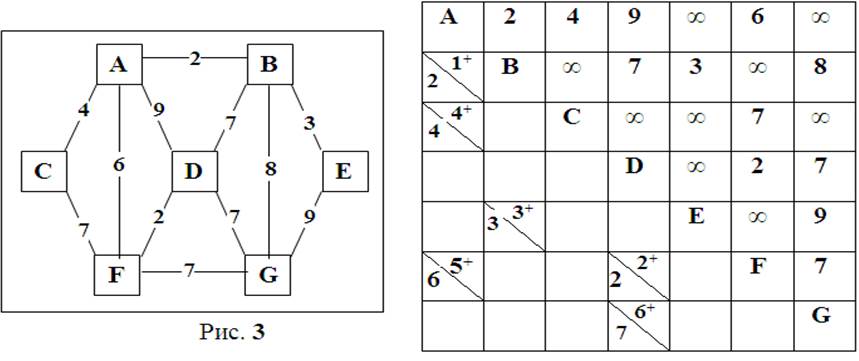
Решение. Построим таблицу Т_* следующим образом.

Запишем в диагональные клетки обозначения вершин A, B, C, D, E F, E.

Над диагональю запишем длины кратчайших путей, но не более чем из одного ребра (в противном случае поставим ∞).

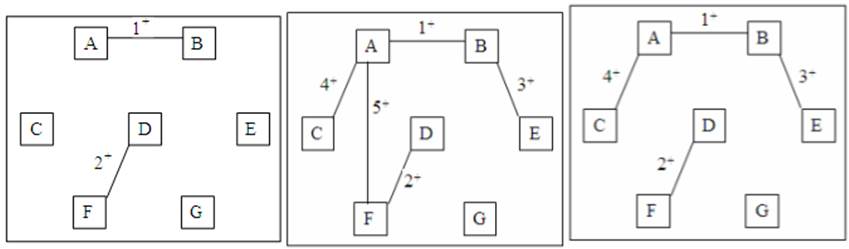
Рис. 4                               Рис. 5                                            Рис. 6

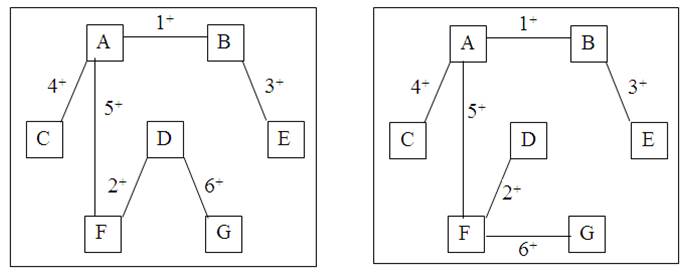
Рис. 7

Под диагональю запишем только  длины ребер минимального дерева .

Начинаем с пустого дерева и добавляем к нему ребра в порядке возрастания их длин, пока не получим набор ребер, объединяющий все вершины графа.

1).Начнем с ребра, имеющего наименьшую длину, т.е. АВ. Запишем над ребром АВ число 1⁺. Затем возьмем ребро DF и запишем над ним число 2⁺ (рис. 4).

2).Добавим ребро длиной 3, соединяющее вершины В и E (3⁺), а затем ребро длиной 4 (4⁺). Мы получим ситуацию, представленную на рис. 5.

3).К результирующему графу добавим ребро длиной 6 (5⁺) (рис.6).